ОСНОВЫ ПОМЕХОУСТОЙЧИВОСТИ
ЧАСТЬ 1
Редактор Т. С. Паршикова
***
Подписано в печать 06.2005 Формат 60 ´ 84 1/16. Бумага офсетная. Плоская печать. Усл. печ. л. 1,5. Уч.-изд. л. 1,7. Тираж 250 экз. Заказ
**
Редакционно-издательский отдел ОмГУПСа Типография ОмГУПСа
*
 644046, г. Омск, пр. Маркса, 35 644046, г. Омск, пр. Маркса, 35
При равенстве априорных вероятностей p(S1) и p(S0) условие (2.2) будет несколько упрощено:
Поскольку функции правдоподобия нами найдены (2.1), то условие (2.3) при работе приемника будет таким:
Здесь необходимо сделать следующее замечание. Так как сигналы y и Si являются функциями времени, их сравнение возможно произвести только в определенный момент времени t0. Такой метод называется приемом по одному отсчету. Вместо экспонент можно сравнивать их показатели и тогда
Если же усреднить по времени левую и правую части (2.5) и разделить на 2σ2, то неравенство принимает следующий вид:
где q(Si) – взаимная корреляция между принимаемым сигналом у и передаваемым Si, а ЕSi– энергия передаваемого сигнала. Если использовать значения входящих в (2.6) выражений q(Si) и ЕSi, то можно установить структурную схему оптимального приемника. Так как при непрерывной обработке
структура оптимального приемника должна содержать звенья, с помощью которых получается две функции (2.7) для каждого сигнала. Далее должно быть решающее устройство, которое определяет, по какой из ветвей обработки имеется максимальный результат, и тому сигналу отдается предпочтение в решении. Это положение иллюстрируется на рис. 2.1.
Рис. 2.1. Структурная схема оптимального приемника
Более определенный вид оптимального приемника будет зависеть от вида принятых сигналов. В качестве примера рассмотрим демодулятор амплитудно-модулированных сигналов: S0 = 0, S1 = A0×cos w0t (см. рис. 2.2).
В итоге получается так, что оптимальный приемник должен анализировать неравенство, которое следует из (2.6):
или
В результате анализа схема рис. 2.1 упрощается и принимает вид, показанный на рис. 2.3
Первые два блока приемника – это коррелятор; полученное значение взаимной корреляции сравнивается с порогом
Так как энергии сигналов равны (Е0 = Е1), то неравенство (2.6) упрощается и критерий проверки сводится к сравнению двух функций корреляции:
Смысл функции корреляции состоит в оценке статистической связи между сигналами. Естественно, с каким из двух сигналов «теснее» связан принимаемый сигнал, тому и должен отдать предпочтение приемник. На рис. 2.5 показана структурная схема оптимального приемника.
Вероятность ошибки как основная характеристика помехоустойчивости будет зависеть не только от интенсивности помех, но и от вида сигналов. Прежде чем сделать какое-то заключение, проведем анализ вероятности ошибки оптимального приемника. При определении вероятности ошибки примем допущение о том, что линия связи канала не дает искажений сигнала и имеет постоянные параметры передачи. Хотя природа сигнала, несущего информацию, случайна, будем считать, что он состоит из элементарных частиц – сигналов, имеющих детерминированный характер за время своего существования. Обратимся к неравенству (2.6) и перепишем его в ином виде:
|



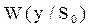
 . (2.3)
. (2.3)

 . (2.4)
. (2.4)
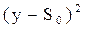
 . (2.5)
. (2.5)

 , (2.6)
, (2.6) , (2.7)
, (2.7)


 . (2.8)
. (2.8)
 0 (2.9)
0 (2.9)
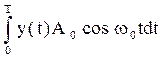
 . (2.10)
. (2.10)

 ). Такой способ приема сигналов при полностью известном передаваемом (а в приемнике – ожидаемом) сигнале называется когерентным.
). Такой способ приема сигналов при полностью известном передаваемом (а в приемнике – ожидаемом) сигнале называется когерентным. Разберем структуру частотного демодулятора: S0 = S×cоsw0t; S1 = S×cоsw1t (см. рис. 2.4).
Разберем структуру частотного демодулятора: S0 = S×cоsw0t; S1 = S×cоsw1t (см. рис. 2.4).

 . (2.11)
. (2.11) Таким образом, на этих двух примерах мы выяснили, что структура приемника зависит от системы применяемых сигналов. Но их вид в системе связи определяет не только это, но и помехоустойчивость связи. Различить при приеме два сигнала S0 = 1 В и S1 = 1,1 В приемнику сложнее, чем сигналы S1 = 1 В и S0 = -1 В.
Таким образом, на этих двух примерах мы выяснили, что структура приемника зависит от системы применяемых сигналов. Но их вид в системе связи определяет не только это, но и помехоустойчивость связи. Различить при приеме два сигнала S0 = 1 В и S1 = 1,1 В приемнику сложнее, чем сигналы S1 = 1 В и S0 = -1 В.



