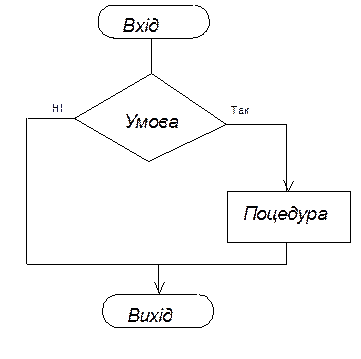Опис алгоритму
· В Профкоме началась запись детей на новогодние утренники. · Новогодний вечер запланирован на 26.12.2013г. в к/т «Октябрь». БУДОВА Й НАЛАГОДЖЕННЯ СИСТЕМ ПРОГРАМНОГО УПРАВЛІННЯ
Спеціальність 5.05050202 "Обслуговування верстатів із програмним управлінням і робототехнічніх комплексів"
Частина 1 "ОСНОВИ ПРОГРАМУВАННЯ МІКРО-ЕОМ МС2102 "
Харків 2013
Методичний посібник з дисцмпліни "Будова й налагодження систем програмногоуправління", частина 1 "Основи програмування мікро-ЕОМ МС2102" для студентів Харківського комп¢ютерно-технологічного коледжу НТУ „ХПІ” спеціальності: 5.05050202 „Обслуговування верстатів із програмним управлінням і робототехнічніх комплексів”. Склав: В.Г. Махотило- викладач методист. Методичний посібник розглянутий і затверджені на засіданні циклової комісії електротехнічних та природо- математичних дисциплін. Протокол № 7 від 15. 02. 2013
Голова комісії __________________ В.Г. Махотило
Заступник директора з навчальної роботи _ХКТК НТУ "ХПІ" _______________ І.І. Дідух ЗМІСТ
1 ПРОЦЕС ПІДГОТОВКИ І РІШЕННЯ ЗАДАЧІ НА ЕОМ.. 4 1.1 Постановка завдання. 4 1.2 Розробка опису завдання. 4 1.3 Алгоритмізація завдання. 4 1.4 Опис алгоритму. 4 1.5 Процеси, що гілкуються. 6 1.6 Циклічні процеси. 8 1.7 Ітераційний цикл. 10 2 ТИПОВІ ОБЧИСЛЮВАЛЬНІ ПРОЦЕДУРИ. 12 2.1. Процедура "ЯКЩО-ТО ІНАКШЕ". 12 2.2 Процедура "ЯКЩО-ТО". 13 2.3. Процедура "РОБИ ДОКИ". 13 2.4. Процедура "ПОВТОРЮЙ ДОКИ". 14 3 ПРОГРАМУВАННЯ МІКРО-ЕОМ МС2102 У МАШИННИХ КОДАХ ПРОЦЕСОРА.. 15 3.1 Блок схема алгоритму. 15 3.2 Приклади складання БСА і програм. 15 3.3 Робота ЕОМ із зовнішнімі пристроями. 24
1 ПРОЦЕС ПІДГОТОВКИ І РІШЕННЯ ЗАДАЧІ НА ЕОМ
Постановка завдання
Для вирішення того або іншого завдання за допомогою ЕОМ необхідно в загальному випадку послідовно виконати наступні основні роботи: 1) розробити опис (бажано математичне) завдання; 2) вибрати (або розробити) математичний метод (алгоритм) рішення задачі; 3) описати обчислювальний процес (скласти блок-схему алгоритму); 4) скласти програму обчислень; 5) ввести програму (і вихідні числа) в пам'ять ЕОМ; 6) оформити документацію програми. В деяких випадках ті або інші роботи виконувати не потрібно.
Розробка опису завдання
Звичайний опис завдання міститься у формулюванні самого завдання. Інколи математичний опис завдання відсутній і його треба розробляти. Математизація завдання зводиться зазвичай до запису завдання у вигляді формул (рівнянні, системи рівнянь, нерівностей і т. п.), визначенню величин початкових даних і послідовності використання формул. Математизацією завдання зазвичай займається інженер-математик або фахівець в тій галузі знань, до якої належить завдання (наприклад, інженер-механік, інженер-технолог і т. п.).
1.3 Алгоритмізація завдання
Алгоритм — це строга послідовність кроків обчислювального процесу, виконання яких наводить від вихідних даних до шуканого результату (тобто рішенню задачі). Алгоритм повинен володіти п'ятьма властивостями: 1) Дискретність. Ця властивість полягає в тому, що алгоритм повинен представляти процес рішення задачі як послідовне виконання простих кроків. При цьому для виконання кожного кроку алгоритму потрібний кінцевий відрізок часу, тобто перетворення вихідних даних в результат здійснюється в часі дискретно. 2) Визначеність. Кожне правило алгоритму має бути чітким, однозначним. 3) Результативність. Алгоритм повинен призводити до вирішення за кінцеве число кроків. 4) Масовість. Алгоритм рішення задачі розробляється в загальному вигляді, тобто він має бути застосовний для деякого класу завдань, що розрізняються лише вихідними даними. 5) Правильність. Алгоритм правильний, якщо його виконання дає правильні результати вирішення поставленої задачі
Опис алгоритму
Алгоритм можна розглядати як план (порядок) обчислень, що описує, як знайти рішення. Цей план можна записати з різною мірою подробиці у вигляді послідовності інструкцій, тобто вказівок: яку операцію і над якими числами потрібно виконати (на кожному кроці рішення задачі). Наприклад, план обчислення 1) ввести (у ЕОМ) конкретне значення х; перейти до виконання наступної по порядку інструкції; 2) обчислити 3) вивести (з ЕОМ) y в, тобто результат; перейти до наступної інструкції; 4) припинити обчислення (кінець). Вочевидь, що без збитку для розуміння обчислювального процесу можна опустити у всіх інструкціях другу половину («перейти до виконання наступної по порядку інструкції»), якщо умовитися, що інструкції виконуються в тому порядку, в якому вони пронумеровані. Зручно представити алгоритм в графічній формі у вигляді блок-схеми. Умовимося змальовувати: - процедуру вводу—виводу у вигляді паралелограма - обчислювальну процедуру у вигляді прямокутника; - початок і кінець алгоритму у вигляді овалу. Усередині кожної фігури (їх називають блоками; звідси і назва "блок-схема алгоритму"- (БСА) записуватимемо конкретний зміст процедури, а самі фігури з'єднаємо між собою лініями зв'язку, що показують послідовність виконання процедур. На рисунку 1, представлена блок-схема алгоритму розглянутого вище завдання.
Рисунок 1-Блок-схема лінійного обчислювального процесу Із зовнішнього вигляду блок-схеми ясно, чому такий обчислювальний процес називають лінійним.
1.5 Процеси, що гілкуються
y= x2+1, якщо х≤0 при заданому значенні х 3x2-х1, якщо х≥0 при заданому значенні х
При складанні блок-схеми цього завдання нам буде потрібно визначити процедуру аналізу х, аби залежно від результату аналізу обчислювати по тій або іншій формулі. Якщо процедуру аналізу х (х —?) позначити ромбом, то блок-схема матиме вигляд рисунок 2а. Такий обчислювальний процес називають таким, що гілкується: залежно від знаку х обчислювальний процес повинен продовжуватися по одній або іншій гілці. Зазвичай процедуру аналізу записують у вигляді процедури перевірки якоїсь умови (наприклад, х > 0?), і залежно від того, виконується ця умова чи ні, обчислювальний процес спрямовують по тій або іншій гілці. Об'єднавши дублюючі процедури, отримаємо блок-схему, представлену на рисунок 2б,
а б Рисунок 2 а і б. Варіанти блок-схеми обчислювального процесу, що розгалужується Пригадаємо, що алгоритм — це строга послідовність кроків (процедур, інструкцій, операцій) обчислювального процесу. Для лінійного процесу порядок їх виконання видно з блок-схеми і стає зовсім ясним, якщо блоки пронумерувати в порядку їх виконання (див. рисунок 1). У таких випадках говорять, що інструкції виконуються в природному порядку (в порядку зростання номерів інструкції). Спробуємо пронумерувати блоки рисунок 2,б. Всього блоків 6. Нумерація перших два (1 і 2) і два останніх (5 і 6) не викликає сумнівів. Пронумеруємо останні блоки так, як показано на рисунок 2, б. Розташуємо блоки послідовно один за одним в порядку зростання їх номерів (рисунок 2б). Відразу видно, що природний порядок (із зростанням номера) виконання блоків тут не дотримується (адже після 2-го виконується 4-й, а після 3-го — 5-й) і це треба якось описати в інструкціях.
Рисунок 5, в і г. Варіант блок схеми процесу, що розгалужується. Процедуру, що виконується блоком 2, можна описати такою інструкцією: «якщо х > 0, то перейти до виконання блоку (інструкції) 4, інакше до наступного по порядку блоку (інструкції), тобто до «3». Якщо умовитися, що при невиконанні умови потрібно завжди переходити до наступної по порядку інструкції, то тоді інструкцію 2 можна записати коротко: «якщо х > 0, то йти до 4». Таку процедуру (операцію) називають умовним переходом, тому що вона описує можливе порушення природного порядку виконання інструкції залежно від результату перевірки умови, записаної в цій інструкції: якщо умова виконується, то переходять до виконання інструкції, номер якому вказаний в самій інструкції (і далі, в природному порядку), якщо ж умова не виконується, то переходять, як завжди, до виконання наступної по порядку інструкції (тобто природний порядок в цьому випадку не порушується). Отже, ми описали одну (праву) гілку рисунок 2в. Як же описується ліва гілка? Стрілка між блоками 3 і 5 вказує на обов'язкове, не обумовлене жодними умовами порушення природного порядку виконання блоків, і наказує перейти до блоку виводу. Це розпорядження записують після блоку 3 зазвичай у вигляді інструкції «йти до...», для якої введемо особливе графічне позначення (усічений зверху і знизу ромб). Вочевидь, цьому блоку потрібно привласнити номер 4 (рисунок 2,г). Поява нового блоку 4 приведе до зсуву номерів подальших блоків на одиницю, і ми отримаємо остаточно блок-схему рисунок 5, г, яку можна описати наступною послідовністю інструкцій: 1. Введення х 2. Якщо х > 0, йти до 5 3. Обчислити в = х2 + 1 4. Йти до 6 5. Обчислити в = 3х2-х 6. Вивід в 7. Кінець Інструкцію «йти до 6» називають операцією безумовного переходу. Вона означає обов'язкове (безумовне) порушення природного порядку виконання інструкції і перехід до виконання тієї інструкції, номер якої вказаний в цій операції. Перехід до виконання іншої інструкції рівносильний передачі управління цієї інструкції. Тому операції умовного п безумовного переходу називають також операціями умовної і безумовної передачі управління.
1.6 Циклічні процеси
Вирішення багатьох завдань полягає в багатократному повторенні обчислень по одних і тих же формулах кожного разу з новими числовими даними. Багато разів виконувану частину обчислювального процесу називають циклом. Розрізняють цикли з лічильником і ітераційні цикли. Цикл з лічильником. Розглянемо завдання: «обчислити суму цілих позитивних чисел від 1 до 100». Вочевидь, потрібно обчислити s = 1 + 2 + 3... + 100; перш ніж складати блок-схему алгоритму, потрібно продумати хід обчислень. Можна передбачити введення всіх доданків 1, 2, 3, 100 і послідовне збільшення їх один до одного. Але, що таке в даному випадку складове? Це величина, яка набуває значень 1, 2, 3, 100 при кожній черговій операції складання. Величину, значення якої міняється в процесі виконання обчислень, називають змінною. Аби звертатися до змінних, їм призначають імена. Призначимо додатку ім'я К. Приписуване змінним конкретних значень зазвичай виробляється за допомогою операції присвоювання, яка записується так: «хай К =...». Наприклад, «хай К = 0». У загальному випадку змінної можна привласнити і значення, що обчислюється якимсь виразом, тобто праворуч від знаку рівності може бути записане не лише якесь число, але і формула. Наприклад, «хай К = К + 1». Вас не повинно бентежити, що цей запис зроблений не по правилах алгебри. Так прийнято писати в інструкціях для ЕОМ і розуміти цю операцію треба так: спочатку в одній інструкції змінної До привласнюється якесь початкове значення, наприклад: «хай К = 0». Якщо далі в іншій інструкції записати «хай До = До + 1». то це означатиме просто «хай К = 1» (адже До дорівнювало 0). Якщо ми знову після цього запишемо «хай К = К + 1», то це означатиме «хай К = 2» (адже К стало вже рівним 1) і т. д., тобто запис «хай К = К + 1» означає, що поточне значення К треба збільшити на одиницю і набутого нового чисельного значення привласнити (приписати) змінній К. Ввівши в машину лише одне початкове значення змінної К (введення К = 0), ми далі за допомогою операції привласнення «хай К=К+1» можемо формувати (отримувати) послідовно всі додатки: 1, 2, 3, 100. Введемо в розгляд ще одну змінну з ім'ям S, початкове значення якої дорівнює 0 (ввод S = 0). Тоді, записавши після операції «хай К = К + 1» операцію «хай S = S + К», ми набудемо нового значення S, рівного сумі початкового значення S (S = 0) і першого додатку (К = 0 + 1 = 1) Після цього потрібно сформувати новий доданок («хай К = К + 1») і додати його до нового значення S («хай S=S + К») і. т.д. Інакше рішення нашої задачі можна описати так. 1. Введення К = 0, S = 0 2. Хай До = К + 1 (здобуття 1-го додатку) 3. Хай S= S + К (збільшення 1-го додатку, рівного 1) 4. Хай К = К + 1 (здобуття 2-го додатку, рівного 2) 5. Хай S = S + К (збільшення 2-го додатку) 200 хай К = K+1 (здобуття 100-го додатку, рівного 100) 201 хай S = S + К (збільшення 100-го додатку) 202 виведення S 203 кінець Ну а якщо нам потрібно знайти суму цілих чисел в діапазоні від 0 до 1000? Записати пару операцій 1000 разів? Частину обчислювального процесу, що повторюється, оформляють як цикл, зазвичай за допомогою операції умовного переходу. В даному випадку ми знаємо точно, скільки разів потрібно повторювати цикл (100 разів). Такий цикл називається цикл з лічильником. Роль лічильника (число циклів) в даному випадку грає змінна К: потрібно цикли виконувати до тих пір, поки К буде менше або рівна 100. Переставивши для зручності інструкції 2 і 3 і додавши умовний перехід, отримаємо: 1) Введення К=0, S=0 2) Хай S=S+K 3) Хай K=K+1 4) Якщо К 5) Виведення S 6) Кінець
Блок-схема такого процесу представлена на рисунок 3.
Рисунок 3 Блок-схема цикала з лічильником При зміні діапазону чисел, наприклад до 1000, нам буде потрібно лише інакше сформулювати четверту інструкцію, а саме записати: якщо К
1.7 Ітераційний цикл
Сформулюємо завдання в загальному вигляді, аби процес рішення можна було використовувати для будь-яких вихідних даних: «обчислити Алгоритм рішення цієї задачі зазвичай ґрунтується на послідовному обчисленні наближень (ітерацій) рішення до тих пір, поки не буде досягнута задана точність, тобто до тих пір, поки Звичайно, аби обчислити друге наближення, потрібно задатися першим (у1) наближенням. У якості у1 можна узяти або 1, або само число N, але найчастіше беруть y1= N/2. Тепер можна обчислити y2 по формулі: Блок-схема алгоритму представлена на рисунок 4. Як бачимо, тут також є цикл, але скільки разів повторюються блоки 3, 4, 5 і 6, ми не знаємо. Умовою виходу з циклу (припинення повторенні) є досягнення заданої точності. Такий цикл називається ітераційним.
Рисунок 4 Блок-схема ітераціонального цикала
Хід обчислень можна записати у вигляді послідовності наступних інструкцій. 1. Ввести N і έ 2. Хай y1 = N/2 3. Обчислити y2=(y1+N/y1)/2 4. Якщо 5. Хай у1 = у2 6. Йти до 3 7. Виведення у2 8. Кінець
2 ТИПОВІ ОБЧИСЛЮВАЛЬНІ ПРОЦЕДУРИ.
2.1. Процедура "ЯКЩО-ТО ІНАКШЕ";
Алгоритм типової обчислювальної процедури "ЯКЩО-ТО ІНАКШЕ" змальоване на рисунок 20.11. Цю процедуру застосовують тоді, коли потрібно реалізувати перехід До однієї з двох обчислювальних процедур залежно від умови. Рисунок 2.1-Алгоритм процедур ЯКЩО-ТО-ІНАКШЕ
2.2 Процедура "ЯКЩО-ТО";
Процедура "ЯКЩО-ТЕ" (рисунок 2.2) є частковим випадком процедури "ЯКЩО-ТЕ ІНАКШЕ" і використовується тоді, коли потрібно реалізувати одну обчислювальну процедуру залежно від умови.
Рисунок 2.2 Алгоритм процедури "ЯКЩО-ТО"
2.3. Процедура "РОБИ ДОКИ";
Процедуру "РОБИ ДОКИ" (рисунок 2.3) використовують для повторення однотипних дій до моменту виконання умови завершення циклу
Рисунок 2.3 Алгоритм програми РОБИ ДОКИ
2.4. Процедура "ПОВТОРЮЙ ДОКИ";
Процедура "ПОВТОРЮЙ ДОКИ" (ПОВТОРЮЙ-ДО-ТОГО-ЯК) (рисунок 2.4) аналогічна передуючою, але однотипні дії виконуються перед перевіркою умови.
Рисунок 2.4 Алгоритм процедури "ПОВТОРЮЙ ДОКИ"
3 ПРОГРАМУВАННЯ МІКРО-ЕОМ МС2102 У МАШИННИХ КОДАХ ПРОЦЕСОРА
|

 при заданому значенні х можна описати наступною послідовністю інструкцій (алгоритм очевидний з самого формулювання завдання):
при заданому значенні х можна описати наступною послідовністю інструкцій (алгоритм очевидний з самого формулювання завдання):
 Розглянемо завдання: обчислити
Розглянемо завдання: обчислити


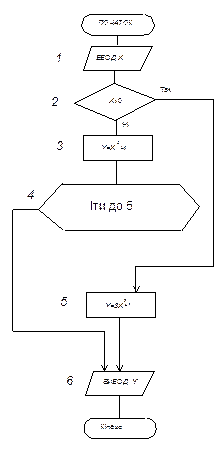
 100, йти до 2
100, йти до 2
 з точністю до έ».
з точністю до έ».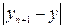 не стане менше έ.
не стане менше έ. (адже у1 нам вже відомо). Якщо ми тепер обчислене значення у2 привласнимо змінною у1 ("хай у2 =у1), то наступне наближення можна обчислити знову за тією ж формулою: і так далі Вочевидь, що після обчислення у2 потрібно перевіряти. Якщо умова не виконується, то потрібно привласнити змінній у1 значення у2 і знову піти на блок обчислення у2; у протилежному ж випадку потрібно піти на блок виведення у2, оскільки виконання умови свідчить про те, що задана точність досягнута.
(адже у1 нам вже відомо). Якщо ми тепер обчислене значення у2 привласнимо змінною у1 ("хай у2 =у1), то наступне наближення можна обчислити знову за тією ж формулою: і так далі Вочевидь, що після обчислення у2 потрібно перевіряти. Якщо умова не виконується, то потрібно привласнити змінній у1 значення у2 і знову піти на блок обчислення у2; у протилежному ж випадку потрібно піти на блок виведення у2, оскільки виконання умови свідчить про те, що задана точність досягнута.
 йти до 7
йти до 7