Экспериментальное определение
Зависимости составляющих сил резания от режимов резания Методика расчета
Зависимость сил резания от режимов резания имеет вид: Рz, x, y =
где v, S, t – скорости, подача и глубина резания; Ср, a, b, g – коэффициент и показатели степени, определяемые экспериментально. Для определения численных значений коэффициента и показателей степени воспользуемся методами линейного регрессионного анализа и планирования эксперимента, которые позволяют получить достоверные данные при минимальном количестве опытов. Прологарифмируем обе части уравнения (1), чтобы привести его к линейному виду: lg P = lg Cp + alg v + blg S + g lg t, (2) и введем обозначения y = lg P; z 1 = lg v; z 2 = lg S; z 3 = lg t (3)
b 0 = lg Cp, b 1 = a, b 2 = b, b 3 = g. (4)
Тогда уравнение (2) примет вид
В уравнении (5) независимые переменные z 1 называются факторами, b 1– параметрами линейной регрессионной модели, величина y – откликом. Каждый фактор принимает только три значения, которые называются уровнями. Для удобства расчетов уровни преобразуются (кодируются) таким образом, что им соответствуют значения –1, 0, +1 (соответственно нижний уровень, средний и верхний). Кодирование производится с помощью уравнений преобразования:
При этом безразмерные факторы x 1, x 2, x 3 удовлетворяют неравенствам:
и равны соответственно
где Пример кодирования факторов приведен в табл. 1.
Таблица 1 Пример кодирования факторов
Выражая теперь величины
Обозначая теперь x 0 = 1,
получим
– линейную регрессионную модель относительно безразмерных факторов x 0, x 1, x 2, x 3. Для нахождения значений параметров модели Условия эксперимента записываются в виде таблицы, где строки соответствуют различным опытам, а столбцы – значениям факторов. Такие таблицы называются матрицами планирования эксперимента. Пример построения матрицы планирования для нашего случая представлен в табл. 2. Таблица 2 Матрица планирования и результаты эксперимента
Примечание: число оборотов в табл. 2 перевести в v (м/мин), в зависимости от диаметра заготовки
Запишем значения факторов xi в матрицу x, а результаты измерений – в вектор-столбец Y. Тогда получим матричную запись уравнения регрессии:
где
Значения параметров
При наличии персонального компьютера данную формулу можно непосредственно программировать на каком-либо языке программирования (Фортран, Си или Паскаль), можно вычислять ее в каком-либо специализированном математическом пакете (Maple, MATLAB или MathCad). Однако при таком выборе матрицы планирования, как в нашем примере, матрица XTX получается диагональной, все вычисления упрощаются так, что их можно проводить с помощью микрокалькулятора. Приведем результаты матричных вычислений, затем формулы для вычисления параметров на калькуляторе.
Значения коэффициентов
где j = 1, 2, 3,..., N – номер опыта; i = 0, 1, 2,..., q – номер фактора. В нашем случае
Далее, зная значения параметров
Таким образом, зависимость технологических сил резания от режимов резания по данным эксперимента определяется выражением: Рz = Срz v a Z S b Z t gZ; Рx = Срx v aX S bХ t gХ; Рy = Срy v aУ S bУ t g x. Кроме того, по повторным наблюдениям можем оценить точность прогноза (дисперсию ошибки) по формуле
где m – число точек в плане,
В нашем примере дисперсия равна 0,8, что соответствует приемлемой точности.
|

 , (1)
, (1) . (5)
. (5)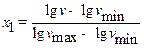 , (6)
, (6) , (7)
, (7) . (8)
. (8) ;
;  ;
; 

 ,
,  ,
,  .
. ,
,  ,
,  из уравнений (6) – (8) через x 1, x 2, x 3 соответственно и подставляя эти выражения в уравнение (5), получим
из уравнений (6) – (8) через x 1, x 2, x 3 соответственно и подставляя эти выражения в уравнение (5), получим (9)
(9)
 (10)
(10)
 (11)
(11) (12)
(12) предусматривается проведение опытов при различных сочетаниях уровней всех трех факторов. Число всех возможных комбинаций для трех факторов равно
предусматривается проведение опытов при различных сочетаниях уровней всех трех факторов. Число всех возможных комбинаций для трех факторов равно  . Обычно берут меньшее количество опытов, например восемь, и четыре опыта для определения погрешности эксперимента.
. Обычно берут меньшее количество опытов, например восемь, и четыре опыта для определения погрешности эксперимента. м/мин.
м/мин. , (13)
, (13)

 .
. находятся по формуле
находятся по формуле . (14)
. (14) ,
,
 ,
, ,
, , (15)
, (15) ;
; ;
; ;
; .
.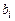 , затем из формулы (4) – значения интересующих нас коэффициентов Ср,
, затем из формулы (4) – значения интересующих нас коэффициентов Ср, 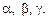
 ;
;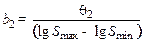 ;
; ;
; .
. ,
,
 – наблюдение в точке плана,
– наблюдение в точке плана,  – среднее значение отклика в точке.
– среднее значение отклика в точке.


