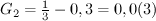Всех жителей некоторой общины можно условно разделить на три равные группы по численности: бедные, средние, богатые. Доход Бедной группы составляет 20% от общего дохода всех жителей данной общины. Доход средней группы составляет 30%. Рассчитайте коэффициент Джини ( ).
).
В общине решили ввести налог на доходы богатой части общества в размере 30% от их дохода. Полученная сумма налога распределяется следующим образом: две трети полученной суммы идет бедным, одна треть - средней группе. Рассчитайте новое значение коэффициенты Джини(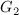 ).
).
Решение: После введения налога доход "богатых" составит:  от общего дохода всех жителей, то есть распределиться между оставшимися группами
от общего дохода всех жителей, то есть распределиться между оставшимися группами 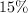 общего дохода, следовательно доходы "бедных" составят:
общего дохода, следовательно доходы "бедных" составят:  ; доходы "средних" составят
; доходы "средних" составят 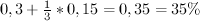 , что равно доходам "богатых", то есть теперь общество делиться на 2 группы: "бедные" (
, что равно доходам "богатых", то есть теперь общество делиться на 2 группы: "бедные" ( населения и
населения и  от общего дохода) и "средние-богатые"(
от общего дохода) и "средние-богатые"( населения и
населения и 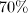 от общего дохода).
от общего дохода).
Коэффициент Джини можно рассчитать, используя лемму о ломаной кривой Лоренца, имеющей два линейных участка (доказательство леммы в задаче, которая называется "В некоторой стране", введите в поиске по сайту, ссылку вставить не получилось), отсюда 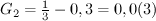
Вычислите коэффициент Джини, примерно отражающий общемировое неравенство доходов, если ВВП развивающихся стран, в которых проживает 80 % населения Земли, в сумме составляют только 20 % общемирового продукта (заметим, что это соотношение держится уже много лет по данным Всемирного банка).
Решение и ответ
j=1-(0,8+(0,2+1))*0.2=1-2*0.2=0.6
Ответ:
0,6

 ).
).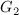 ).
). от общего дохода всех жителей, то есть распределиться между оставшимися группами
от общего дохода всех жителей, то есть распределиться между оставшимися группами 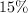 общего дохода, следовательно доходы "бедных" составят:
общего дохода, следовательно доходы "бедных" составят:  ; доходы "средних" составят
; доходы "средних" составят 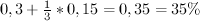 , что равно доходам "богатых", то есть теперь общество делиться на 2 группы: "бедные" (
, что равно доходам "богатых", то есть теперь общество делиться на 2 группы: "бедные" ( населения и
населения и  от общего дохода) и "средние-богатые"(
от общего дохода) и "средние-богатые"( населения и
населения и 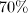 от общего дохода).
от общего дохода).