Оптимізаційні моделі в маркетингу
Оптимізаційними задачами в економіці називають економіко-математичні задачі, ціль яких - знаходження найкращого (оптимального) з позиції деякого критерію (критеріїв) варіанта використання ресурсів. Вирішуються такі задачі за допомогою оптимізаційних моделей методами математичного програмування. Оптимізаційні моделі крім рівнянь або нерівностей, які описують взаємозв'язки між змінними,містять також критерій для вибору - функціонал або цільову функцію, що набирає значення в межах області припустимих рішень. Цільова функція в загальному вигляді визначається трьома моментами: керованими змінними, некерованими параметрами (що залежать, наприклад, від зовнішнього середовища) і формою залежності між ними (виглядом функції). Якщо позначитикритерій оптимальності через U, керовані змінні - X,параметри - Р,задані межі (область) зміни керованих змінних - через М, то загальний вигляд оптимізаційної моделі буде таким:
Задачі вигляду (4.1) розв'язуються методами математичного програмування, що включає в себе лінійне програмування, нелінійне програмування, динамічне програмування, цілочисельне програмування і т. д. Вибірметодів математичного програмування для розв'язання оптимізаційних задач визначається виглядом цільової функції, виглядом обмежень, що визначають область М, і спеціальнимиобмеженнями на керовані змінні (наприклад, вимогою щодо їх цілочисельності). Рішення задачі (4.1) звичайно називається оптимальним рішенням, або оптимальним планом. Оптимізаційні задачі, які можуть бути зведені до задач лінійного програмування (ЗЛП), можуть бути сформульовані, наприклад, таким чином: знайти вектор
і задовольняє лінійним функціональним обмеженням:
і прямим обмеженням:
Значна частина економічних задач, у тому числі й у галузі маркетингу,потребує цілочисельного рішення, коли змінні величини означають кількість неподільних одиниць продукції, обладнання тощо. В ряді випадків такі задачі вирішуються з використанням звичайних методів, наприклад симплексного, з подальшим округленням до цілих чисел або за методом Гоморі для лінійних задач цілочисельного програмування. Розглянемо детальніше найбільш розповсюджені види оптимізаційних моделей. Статична модель оптимізації прикріплення споживачів до постачальників. Основною математичною моделлю оптимального прикріплення споживачів до постачальників є так звана транспортна задача лінійного програмування, яка дозволяє скласти такий план прикріплення споживачів до постачальників (план перевезень), за якого загальна величина транспортних витрат є мінімальною. Цільова функція має вигляд:
при обмеженнях:
де Обмеження означають повне задоволення попиту у всіх пунктах споживання і повне вивезення продукції від усіх постачальників. Необхідною і достатньою умовою розв’язання задачі є збереження балансу:
Модель оптимального складання сумішей. Модель може бути використана, коли процес виробництва готової продукції пов’язаний із сполученням кількох компонентів. При цьому якість готової продукції має відповідати певним вимогам при досягненні максимального економічного ефекту. У загальному вигляді задача формулюється наступним чином. Якщо склад готової продукції включає m елементів, лімітованих величиною li (i-1,…,m), то для елементів, що погіршують якість продукції вводиться аi - верхня межа присутності у суміші, а для елементів, що поліпшують якісь – нижня межа. Обсяги окремих п компонентів, які використовуються у виробничому процесі, обмежуються величиною bj. Вміст кожного елемента у певному компоненті позначається через аij, вартість окремих компонентів (включаючи витрати на переробку) – через сj, плановий обсяг виробництва – через М. Потрібно скласти таку суміш з наявних компонентів, щоб витрати на її складання були мінімальні. Цільова функція має вигляд:
при обмеженнях:
Модель оптимального розкрою матеріалів. Може бути застосована при складанні оптимального технологічно припустимого плану розкрою із стандартних одиниць ресурсів, за якого при виготовленні необхідного набору заготівок мінімізується загальна величина відходів крою або кількість одиниць ресурсів, які підлягають розкрою. Цільова функція задачі оптимального розкрою за одним виміром довгомірних матеріалів за критерієм мінімуму відходів матиме вигляд:
За критерієм мінімуму одиниць розкрою:
за умов:
Вихідними умовами для складання варіантів розкрою є такі:
Моделі раціонального розподілення матеріальних ресурсів. Може бути використана у випадках, коли перед службою маркетингу постає задача раціонального розподілення різних видів матеріальних ресурсів за умови максимізації прибутку, обсягів виробництва товарів підвищеного попиту, мінімізації виробничих та інших витрат. У загальному вигляді задача може бути сформульована так. Обсяги m видів вихідних матеріальних ресурсів обмежені величиною аі; і=1,…,т. З них випускається п видів продукції мінімальним обсягом bj; j=1,…,n. Норми витрат певного ресурсу на виробництво одиниці продукції певного виду аij, а також прибуток, отримуваний від реалізації одиниці продукції певного виду cj, є фіксованими і не залежать від обсягів випуску продукції. Потрібно скласти план розподілення вихідних матеріальних ресурсів, який максимізує суму прибутку від реалізації усієї продукції або мінімізує загальну собівартість виготовленої продукції. У першому випадку цільова функція буде мати вигляд:
у другому:
де s – собівартість виробництва одиниці продукції певного виду. Обмеження на ресурси, план виробництва і тривіальні виглядають так:
|

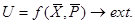 (4.1)
(4.1)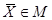
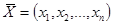 , який максимізує лінійну цільову функцію:
, який максимізує лінійну цільову функцію: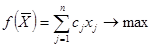
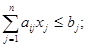
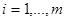
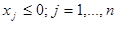
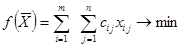
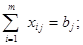
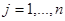
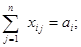
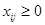
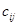 - витрати на перевезення одиниці продукту від постачальника до споживача;
- витрати на перевезення одиниці продукту від постачальника до споживача; 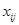 - кількість продукту, перевезеного від постачальника до споживача;
- кількість продукту, перевезеного від постачальника до споживача; 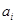 - кількість продукту, зосередженого у постачальника;
- кількість продукту, зосередженого у постачальника;  - обсяг споживання споживача.
- обсяг споживання споживача.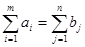
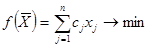
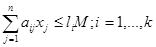
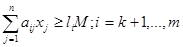
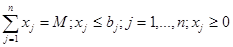 .
.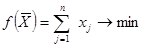
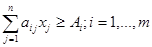
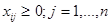 .
.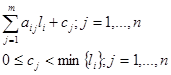
 ,
,