Алгоритм метода Эйлера
(ответственность, исполнительность, дисциплинированность, активность, инициативность, творчество, взаимоотношения и пр., проявленные (или не проявленные) студентом в ходе практики) ___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ По итогам прохождения практики студент(ка) получает «зачёт» (количество баллов – ____), «незачёт» (количество баллов – ____) Подпись руководителя практики ________________________
Дата«____» _____________ 201_г. Данная страница Дневника после заполнения преподавателем распечатывается и прикладывается к итоговому отчёту по практике на заседании кафедры методики технологического образования.
Отчеты По ЧИСЛЕНННЫМ МЕТОДАМ Выполнил:студент гр. 4111-71 Юсупова Р.И. Проверила:доцент каф. хим. кибернетики Кошкина Л.Ю.
Казань, 2012 Содержание Тема 1. «Численное реш е ния дифференциальных уравнений». 3 Постановка задачи. 3 Решение: Одношаговые методы …………………………………………………………………..3 Листинг программ………………………………………………………………………….5 Результаты.. 5 Вывод. 5 Список литературы.. 5
ТЕМА 1. «ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ» Постановка задачи 1) Решить дифференциальное уравнение:
при
2) Решить систему обыкновенных дифференциальных уравнений:
dz/dx=3y-2z
z0 =10
Для решения уравнения использовали следующие методы: 1. метод Эйлера, 2. метод Рунге-Кутта. Решение: Одношаговые методы 1) Метод Эйлера: Алгоритм метода Эйлера
На каждом шаге погрешность имеет порядок Метод имеет первый порядок точности. Он используется сравнительно редко.
|


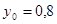
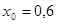
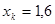

 dy/dx=-2yx+z
dy/dx=-2yx+z
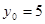
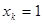
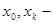 конец интервала;
конец интервала;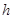 -шаг интегрирования;
-шаг интегрирования; начальное условие;
начальное условие;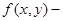 правая часть уравнения.
правая часть уравнения.
 Ввод
Ввод 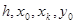
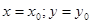

 Начало цикла
Начало цикла
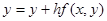

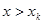
 .При нахождении решения в точке
.При нахождении решения в точке 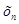 ,относящейся от
,относящейся от  на расстояние L,погрешность суммируется. Суммарная (глобальная) погрешность на n-ном шаге равна
на расстояние L,погрешность суммируется. Суммарная (глобальная) погрешность на n-ном шаге равна 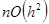 . Так как h=L/n,то
. Так как h=L/n,то 



