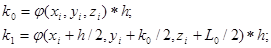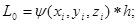Function f1(x, y, z)

f1 = -2 * y * x + z

End Function

 

Function f2(x, y, z)

f2 = 3 * y - 2 * z

End Function

 

Sub metod_dv_Eilera()

x = 0

xk = 1

y = 5

z = 10

h = 0.1

i = 2

Do

y = y + h * f1(x, y, z)

z = z + h * f2(x, y, z)

x = x + h

With Worksheets("Лист2")

.Cells(i, 1).Value = x

.Cells(i, 2).Value = y

.Cells(i, 3).Value = z

End With

i = i + 1

Loop While x < xk

End Sub

 

Sub metod_dv_Runge_Cutta()

x = 0

xk = 1

y = 5

z = 10

h = 0.1

i = 2

Do

k0 = f1(x, y, z) * h

k1 = f1(x + h / 2, y + k0 / 2, z + m0 / 2) * h

k2 = f1(x + h / 2, y + k1 / 2, z + m1 / 2) * h

k3 = f1(x + h, y + k2, z + m2) * h

y = y + (k0 + 2 * k1 + 2 * k2 + k3) / 6

 

m0 = f2(x, y, z) * h

m1 = f2(x + h / 2, y + k0 / 2, z + m0 / 2) * h

m2 = f2(x + h / 2, y + k1 / 2, z + m1 / 2) * h

m3 = f2(x + h, y + k2, z + m2) * h

z = z + (m0 + 2 * m1 + 2 * m2 + m3) / 6

 

x = x + h

With Worksheets("Лист2")

.Cells(i, 5).Value = x

.Cells(i, 6).Value = y

.Cells(i, 7).Value = z

End With

i = i + 1

Loop While x < xk

End Sub

 

Для запуска программ нажать на кнопку или на Run.

Полученный результат находится на Листе 1.

Результаты

1)

x	y		x	y
0,7	0,956817		0,7	0,961144
0,8	1,122274		0,8	1,130719
0,9	1,296043		0,9	1,30837
	1,477761			1,493711
1,1	1,667039		1,1	1,686329
1,2	1,863463		1,2	1,885794
1,3	2,066597		1,3	2,091657
1,4	2,275992		1,4	2,303463
1,5	2,491191		1,5	2,52075
1,6	2,711732		1,6	2,743065
метод Эйлера		Метод Рунге-Кутта

 

2)

x	y	z		x	y	z
0,1		9,8		0,1	5,943607	9,938689
0,2	6,86	9,898		0,2	6,739946	10,08523
0,3	7,5754	10,19102		0,3	7,398777	10,36509
0,4	8,139978	10,59481		0,4	7,910446	10,71269
0,5	8,548261	11,04033		0,5	8,268516	11,07302
0,6	8,797467	11,4715		0,6	8,471084	11,40113
0,7	8,888921	11,84388		0,7	8,521459	11,66185
0,8	8,82886	12,12376		0,8	8,428272	11,82947
0,9	8,628618	12,28759		0,9	8,205051	11,88733
	8,304226	12,32134			7,869364	11,82715
1,1	7,875515	12,21973		1,1	7,441647	11,64816
Метод Эйлера			Метод рунге-Кутта

 

Вывод:

Оба метода являются одношаговыми. Метод Эйлера имеет первый порядок точности. Он используется сравнительно редко. Метод Рунге-Кутта является наиболее распространенным методом решения обыкновенных дифференциальных уравнений.

Сравним время решения дифференциального уравнения по методу Эйлера и Рунге-Кутта. Если мы уменьшим шаг h в два раза, то т.к. метод Рунге-Кутта имеет порядок точности , погрешность уменьшится примерно в 16 раз. Так как на каждом шаге правая часть уравнения вычисляется 4 раза, то количество вычислений увеличится в 8 раз. Чтобы уменьшить погрешность вычисления по методу Эйлера в 16 раз, надо шаг уменьшить в 16 раз, а значит, в столько же раз увеличится количество вычислений правой части. Значит, для метода Рунге-Кутта потребуется в два раза меньше времени вычисления. Кроме того, при вычислении с шагом h точность решения методом Рунге-Кутта была выше. При уменьшении шага в большее число раз получим еще больший выигрыш во времени вычислений.

Особенность одношаговых методов в том, что для получения решения в каждом новом расчетном узле достаточно иметь значения сеточной функции лишь в предыдущем узле. Это позволяет непосредственно начать счет при i=0 по известным начальным значениям. Это допускает изменение шага в любой точке в процессе расчета. Недостатком одношаговых методов является трудность выбора шага, т.к. трудно вычислить погрешность на каждом шаге.

Приведем формулы Рунге-Кутта для системы двух уравнений:

c начальными условиями: при

Формулы имеют вид:

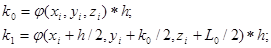
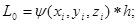
Аналогично можно записать формулы Рунге-Кутта для систем из трех и более уравнений. Алгоритм решения аналогичен алгоритму решения системы уравнений методом Эйлера.

 

Список литературы

 

1. Лекции по численным методам доцента кафедры химической кибернетики КНИТУ Кошкиной Л.Ю.

2. Кошкина Л.Ю. и др. Вычислительная математика в среде Excel: Методические указания. Часть 2. / Казан. гос. технол. ун-т; Казань, 2003, с. 72

3. Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании: Учебное пособие. – М.: Финансы и статистика, 2001.-256 с:ил.

4. Рено Н.Н. Численные методы. Учебное пособие / Казан. гос. технол. университет; Казань,2007, 112 с.

5. Турчак Л.И. Основы численных методов. - М.: Наука, 1987. – 318 с.

6. Дьяконов В.П. Справочник по алгоритмам и программам на языке бейсик для персональных ЭВМ: Справочник. – М.: Наука.1989. –240 с.

7. Назаров С.В., Мельников П.П. Программирование на MS Visual Basic: Учебное пособие / Под ред. С.В. Назарова. – М.: Финансы и статистика, 2001. – 320 с.: ил.