Системы n линейных уравнений c n неизвестными.
Общий вид системы уравнений (m=n):
Матрица А такой системы является квадратной: А=
Метод Крамера Теорема (правило Крамера). Пусть Δ; — определитель матрицы — определитель матрицы системы А, а Δ; j — определитель, полученный из определителя Δ;заменой j-го столбца столбцом свободных членов В. Тогда, если Δ xi = Δj / Δ;, j= 1,2,…,n. (7) Формулы вычисления неизвестных (7) носят название формул Крамера. Правило Крамера можно использовать, только когда определитель системы Δ;не равен нулю. Пример: Решить, используя правило Крамера, систему уравнений:
Решение: Δ= Вычислим дополнительные определители и значения неизвестных: Δ1= Δ2= Δ3= Путем подстановки можно проверить, что полученное решение Х=(2,-1,1) является верным. Контрольные вопросы (ОК-1, ОК-2, ОК-11, ПК-1): 1. Что такое определитель системы линейных уравнений? 2. Какие системы называются совместными, несовместными, определёнными, неопределёнными, однородными, неоднородными? 3. Что такое решение системы? 4. Приведите формулы Крамера для решения систем линейных уравнений 5. Какие системы могут быть решены по формулам Крамера?
Практические задания общие (ОК-1, ОК-2, ОК-11, ПК-1): Пример 1. ( ОК-1, ОК-2, ОК-11): Решить систему
Решение: Вычислим определитель основной матрицы системы: Оставим без изменения первую строку (здесь элемент а11 =1). Получим в первом столбце нули. Воспользуемся свойством 7. Сначала элементы 1-ой строки умножим на (-2) и сложим полученные элементы со 2-ой строкой. Затем умножим элементы 1-ой строки на (-3) и сложим с 3-ей строкой. Умножим на (-1) и сложим с 4-ой строкой. Получим определитель, в котором в 1-ом столбце все элементы, кроме а11, равны нулю. Проведем разложение по первому столбцу.
= Так как Вычисляем определители:
Следовательно, х1 = х3 = Замечание. В случае, когда число неизвестных n велико, практическое использование формул Крамера затруднено в связи с необходимостью большого числа вычислений. Кроме того, что самое главное, в случае, когда коэффициенты уравнений системы заданы приближенно (в практических задачах бывает почти всегда), погрешность решения может быть весьма велика. Поэтому при практическом решении системы уравнений формулы Крамера используют редко. 2. Решить систему по формулам Крамера 3. Решить системы уравнений методом Крамера ( ОК-1, ОК-2, ОК-11): а) г) Индивидуальные задания ( ОК-1, ОК-2, ОК-11, ПК-1): №1. Решите системы линейных уравнений, применяя метод Крамера: 1. 3. 4. 6. 8. 10. Рекомендуемое содержание отчета (для студента). 1. Название лабораторной работы 2. Цель и задачи исследований 3. Электронно-вычислительные средства для расчетов 4. Журнал (тетрадь) исследований (вычислений) с обработкой полученных данных в виде таблиц, графиков (по требованию) 5. Выводы 6. Анализ и защита лабораторной работы производится по результатам представленного студенческой группой отчета (перечень сделанного, рекомендации, ответы на рассмотренные в процессе выполнения контрольные вопросы) Преподаватель оценивает знание каждого студента.
Литература
|

 (4).
(4). (5) и она имеет определитель Δ, который называется определителем системы.
(5) и она имеет определитель Δ, который называется определителем системы. 0, тосистема линейных уравнений (4) имеет единственное решение, определяемое по формулам
0, тосистема линейных уравнений (4) имеет единственное решение, определяемое по формулам
 =
=  =
=  =-11
=-11  =
=  = -
= -  =-22; x 1 = Δ;1 / Δ; = (-22)/(-11)= 2.
=-22; x 1 = Δ;1 / Δ; = (-22)/(-11)= 2. =
=  =
=  =11; x2 = Δ2 / Δ; = 11/(-11)=-1.
=11; x2 = Δ2 / Δ; = 11/(-11)=-1. =
=  =
=  =-11; x 3 = Δ;3 / Δ; = (-11)/(-11)=1.
=-11; x 3 = Δ;3 / Δ; = (-11)/(-11)=1.


 =35 ≠ 0, то система имеет единственное решение и формулы Крамера можно применить.
=35 ≠ 0, то система имеет единственное решение и формулы Крамера можно применить. ;
;  ;
; ;
;  .
. =
=  = 2, х2 =
= 2, х2 =  =
=  = - 1,
= - 1, =
=  = 0, х4 =
= 0, х4 =  =
=  = - 2.
= - 2. ( ОК-1, ОК-2, ОК-11)
( ОК-1, ОК-2, ОК-11) б)
б)  в)
в) 
 д)
д) 
 2.
2. 

 5.
5. 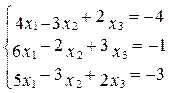
 7.
7. 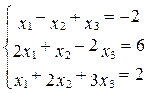
 9.
9. 




