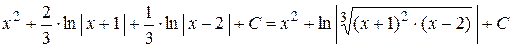Метод неопределенных коэффициентов
Пусть требуется вычислить интеграл от правильной дроби, знаменатель которой имеет вид
В этом случае следует разложить подынтегральную функцию на элементарные дроби:
Неопределённые коэффициенты
Пример. Найти интеграл Решение. Представим дробь
Для того чтобы найти неизвестные величины A и B, умножим это выражение на знаменатель левой части
Приравняем коэффициенты при одинаковых степенях х в левой и правой частях, получим систему линейных уравнений
Её решения:
Пример. Найти интеграл Решение. Подынтегральная функция является неправильной рациональной дробью. Разделим числитель на знаменатель «уголком»
Получим
Разложим знаменатель правильной дроби на элементарные сомножители:
Теперь разложим правильную дробь на элементарные дроби:
Для того чтобы найти неизвестные величины A и B, умножим это выражение на знаменатель левой части
Приравняем коэффициенты при одинаковых степенях х в левой и правой частях, получим систему линейных уравнений
Решения системы:
Итак,
=
|
.
.
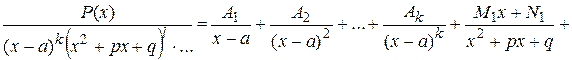
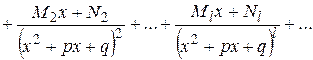находят из последнего равенства, домножив его на знаменатель левой части. Тем самым получается равенство двух многочленов. А, как известно, два многочлена равны тогда, когда равны коэффициенты при одинаковых степенях неизвестной величины. Поэтому приравнивают коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества и решают систему линейных уравнений относительно коэффициентов 
.
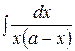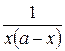в виде суммы двух дробей:
+ 
.
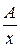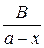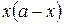. Получим равенство многочленов:
.
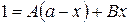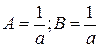. Следовательно,
.
.
.
= 
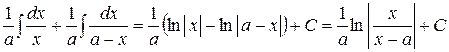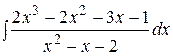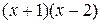, тогда
.
= 
+ 
.
.
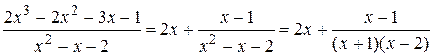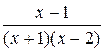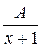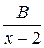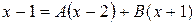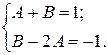
. Следовательно,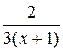
+ 
;
.
=
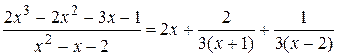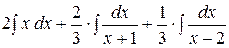