Интегрирование тригонометрических функций
Если подынтегральная функция в неопределённом интеграле является тригонометрической, то её преобразуют с помощью тригонометрических формул к табличному виду, или используют различные подстановки. При выборе подстановок для вычисления интеграла вида
где R – рациональная функция, рекомендуется использовать следующие правила. 1. Если
2. Если 3. Если
4. Универсальная тригонометрическая подстановка
Пример. Найти интеграл Решение. Применим универсальную тригонометрическую подстановку
= Пример. Найти интеграл Решение. Подынтегральная функция является чётной, поэтому применив подстановку
Контрольные вопросы: 1. В чем заключается непосредственное интегрирование? 2. В чем заключается метод интегрирования с помощью замены переменной в неопределенном интеграле? 3. В каких случаях применяется формула интегрирования по частям? 4. В чем заключается интегрирование рациональных функций? 5. В чем заключается метод неопределенных коэффициентов? 6. В чем заключается интегрирование иррациональных функций? 7. В чем заключается интегрирование тригонометрических функций?
Литература: 1. Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н.Фридман. Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2005. – 471 с. 2. Общий курс высшей математики для экономистов: Учебник. / Под ред. В.И. Ермакова. –М.: ИНФРА-М, 2006. – 655 с. 3. Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред.В.И. Ермакова. М.: ИНФРА-М, 2006. – 574 с. 4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1, 2. – М.: Оникс 21 век: Мир и образование, 2005. – 304 с. Ч. 1; – 416 с. Ч. 2. 5. Математика в экономике: Учебник: В 2-х ч. / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандара. – М.: Финансы и статистика, 2006. 6. Шипачев В.С. Высшая математика: Учебник для студ. вузов – М.: Высшая школа, 2007. – 479 с.
|

 ,
,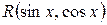 - нечётная функция относительно sin x, то интеграл преобразуется к интегралу от рациональных функций с помощью подстановки
- нечётная функция относительно sin x, то интеграл преобразуется к интегралу от рациональных функций с помощью подстановки 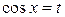 .
. .
. . При этом имеем:
. При этом имеем: , откуда
, откуда  ;
; ;
;  .
. сводит интеграл к интегралу от рациональной функции. При этом имеем:
сводит интеграл к интегралу от рациональной функции. При этом имеем: , откуда
, откуда  ;
;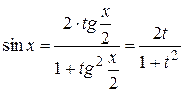 ;
; 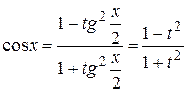 .
.  .
. .
.
 .
. .
. .
.


