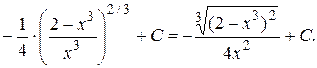Интегрирование иррациональных функций
Интегралы от иррациональных функций обычно приводят с помощью соответствующих замен или преобразований к интегралам от рациональных функций или сразу к табличным интегралам. При выборе методов решения полезны следующие правила.
1. Интегралы вида
где R – рациональная функция; преобразуются к интегралам от рациональных функций с помощью подстановки Пример. Найти интеграл Решение. Подынтегральная функция является иррациональной функцией. Сделаем замену
Подынтегральная функция полученного интеграла является неправильной рациональной дробью. Разделив числитель на знаменатель, получим
откуда
2. Интегралы вида
3. Интегралы вида
= из которых первый – табличный, а второй рассмотрен выше.
Пример. Найти интеграл Решение. Аналогично вычислению интеграла III типа от рациональной функции, выполним три вспомогательных действия. 1) Обозначим квадратный трехчлен, стоящий под знаком корня, через 2) Выделим в числителе дроби производную знаменателя:
3) Выделим в знаменателе дроби полный квадрат:
Тогда исходный интеграл можно представить в виде суммы двух интегралов
Первый из полученных интегралов вычислим с помощью замены
4. Для интегралов вида 1) p – целое число, тогда интеграл сводится к интегралу от рациональной функции с помощью подстановки 2) 3) Пример. Найти интеграл Решение. Заданный интеграл можно представить в виде:
Тогда m = -3, a = 2, b = -1, n =3, p = -1/3; p
Преобразуем подынтегральное выражение следующим образом:
тогда
=
|

 ,
,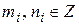 ,
, 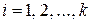 ,
, , где s – наименьшее общее кратное чисел
, где s – наименьшее общее кратное чисел 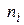 .
. .
.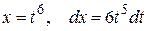 , откуда
, откуда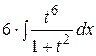 .
. ,
, =
= 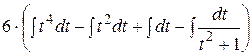 =
=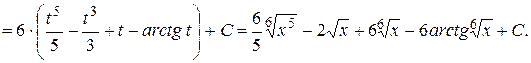
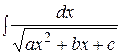 путём выделения полного квадрата из квадратного трехчлена приводятся к табличным интегралам
путём выделения полного квадрата из квадратного трехчлена приводятся к табличным интегралам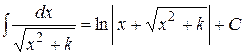 или
или  .
.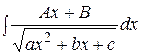 путём выделения в числителе производной квадратного трехчлена, стоящего под знаком корня, раскладывают на сумму двух интегралов
путём выделения в числителе производной квадратного трехчлена, стоящего под знаком корня, раскладывают на сумму двух интегралов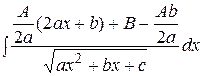 =
=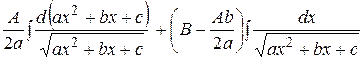 ,
,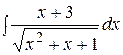 .
.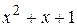 = t 2, откуда, дифференцируя, получим
= t 2, откуда, дифференцируя, получим 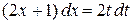 , или
, или 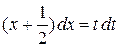 .
.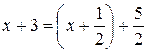 .
.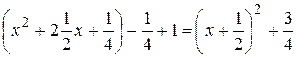 .
.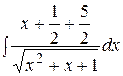 =
= 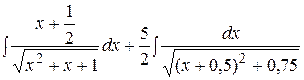 .
.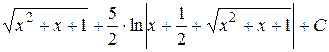 .
. , где m, n, p – рациональные числа, точное решение может быть найдено только в трёх случаях:
, где m, n, p – рациональные числа, точное решение может быть найдено только в трёх случаях: , где s – наименьшее общее кратное знаменателей дробей m и n;
, где s – наименьшее общее кратное знаменателей дробей m и n;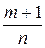 – целое число, тогда интеграл сводится к интегралу от рациональной функции с помощью подстановки
– целое число, тогда интеграл сводится к интегралу от рациональной функции с помощью подстановки 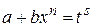 , где s – наименьшее общее кратное знаменателей дробей m и n;
, где s – наименьшее общее кратное знаменателей дробей m и n; – целое число, тогда интеграл сводится к интегралу от рациональной функции с помощью подстановки
– целое число, тогда интеграл сводится к интегралу от рациональной функции с помощью подстановки  , где s – знаменатель дроби p.
, где s – знаменатель дроби p.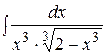 .
.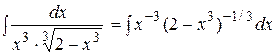 .
. Z,
Z, 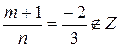 ,
,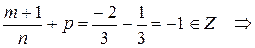 используем подстановку
используем подстановку 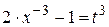 , откуда, дифференцируя, получим
, откуда, дифференцируя, получим  , или
, или 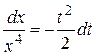 .
.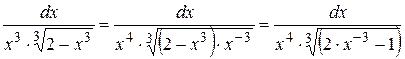 ,
,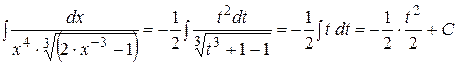 =
=