Интегрирование рациональных функцийВыражение вида Рациональная дробь называется правильной, если m < n, и неправильной, если m Если дробь неправильная, то делением многочлена Элементарными дробями называют правильные дроби следующих видов: I. III. IV. A, B, p, q, a – действительные числа. Интегралы от элементарных дробей можно вычислить следующим образом. I. II. III. Для вычисления интеграла 1) Обозначим знаменатель дроби 2) Выделим в числителе дроби производную знаменателя:
3) Выделим в знаменателе дроби полный квадрат:
Тогда исходный интеграл можно представить в виде суммы двух интегралов, из которых первый можно вычислить заменой
+ = IV. Аналогично предыдущему случаю интеграл можно представить в виде суммы двух интегралов
из которых первый найдём с помощью замены
Обозначив
Интеграл
которая после (n - 1)-кратного применения сводит исходный интеграл
Пример. Найти интеграл Решение. Данный интеграл является интегралом III типа. Выделив в знаменателе полный квадрат, приведём интеграл к табличному интегралу.
Пример. Найти интеграл Решение. Данный интеграл является интегралом III типа. Выполним три вспомогательных действия. 1) Обозначим знаменатель дроби 2) Выделим в числителе дроби производную знаменателя:
3) Выделим в знаменателе дроби полный квадрат:
Тогда исходный интеграл можно представить в виде суммы двух интегралов
из которых первый найдём с помощью замены
|
, где 
, 
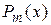- многочлены степени m и n соответственно, называется рациональной дробью (рациональной функцией).
n.
; II. 
, где 
;
, где 
;
, где 
,
;
;
выполним три вспомогательных действия.
= t, откуда, дифференцируя, имеем 
, или 
.
.
.
.
= 
,
= 
.
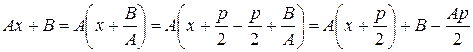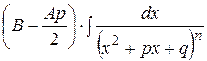, получим
.
вычисляется по рекуррентной формуле: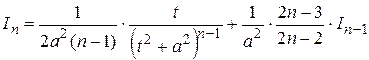
,
к табличному интегралу
.
.
.
= t, откуда, дифференцируя, имеем 
, или 
.
.
.
6 
,
.
