Формула интегрирования по частям
Пусть u = u (x) и v = v (x) — дифференцируемые на некотором промежутке X функции. Тогда
Интегрируя это выражение, получим:
откуда следует формула интегрирования по частям:
С помощью формулы (1) нахождение интеграла Для интегралов вида Для интегралов вида
Пример. Найти неопределенный интеграл
Решение. Пусть u = x; dv = cos 3 x dx, тогда du = dx; v =
Пример. Найти неопределенный интеграл ò (x2 – 3 x + 2) e5xdx. Решение. Пусть x2 – 3 x + 2 = u; e5xdx = dv. Тогда du = (2 x – 3) dx; ò (x2 – 3 x + 2) e5xdx = К последнему интегралу ещё раз применим метод интегрирования по частям, полагая 2 x - 3 = u; e5xdx = dv. Отсюда следует: du = 2 dx; ò (x2 – 3 x + 2) e5x dx =
Пример. Найти неопределенный интеграл Решение. Пусть тогда
|

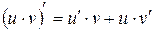 .
. ,
, ,
, = uv –
= uv –  . (1)
. (1)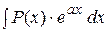 ,
,  ,
,  , где
, где  - многочлен, за u следует принять
- многочлен, за u следует принять  ,
, 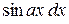 ,
,  .
. ,
,  ,
,  , где
, где  ,
,  ,
,  , а за dv –
, а за dv –  .
. sin 3 x. Отсюда по формуле интегрирования по частям получим:
sin 3 x. Отсюда по формуле интегрирования по частям получим:
 . По формуле интегрирования по частям получим:
. По формуле интегрирования по частям получим: .
.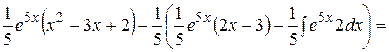
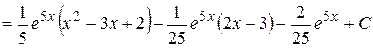 .
. .
. ,
,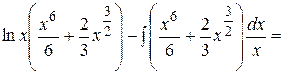
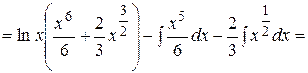
 .
.


