Численные методы оптимизации

М.ғ.д., профессор Қуракбаев Қ.К.

 

 

Как вернуться на общую систему с УСН

 

Без уведомления инспекции вернуться на общую систему с УСН нельзя. Инспекцию надо уведомить, независимо от причин ухода с упрощенки.

 

Если компания сама хочет со следующего года уйти со спецрежима (УСН), то уведомление надо направить не позднее 15 января 2016 года (п. 1, 3 ст. 346.13 НК РФ). Пример заполнения уведомления об отказе от применения упрощенки смотрите ниже. Иначе организация останется на спецрежиме. Если компания в середине года превысила лимит по доходам, то и об этом надо сообщить инспекторам. Срок - 15 календарных дней с окончания квартала, в котором превышены доходы (п. 5 ст. 346.13 НК РФ). Иначе возможен штраф 200 рублей (ст. 126 НК РФ).

Пример заполнения уведомления об отказе от применения упрощенки

на 2 странице (внизу)

 

Источник: http://www.gazeta-unp.ru/news/13559-kak-vernutsya-na-obshchuyu-sistemu-s-usn#ixzz3lhK9WCUt

Численные методы оптимизации

Многие (почти все) задачи оптимизации, какими бы способами они ни решались в конце концов сводятся к задаче минимизации функции многих переменных

(1)

В качестве могут быть проектные параметры приборов и технологических процессов, элементы матриц оптимизируемых функционалов, начальные условия для множителей Лагранжа и др. Здесь – допустимое значение множества изменения параметров .

Точка называется точкой глобального минимума , если для всех выполняется неравенство

для всех

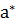Точка называется точкой локального минимума функции , если существует - окрестность точки : (, такая, что для всех .

Если допустимое множество в задаче минимизации совпадает со всем пространством , то говорят о задаче безусловной оптимизации

(2)