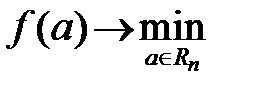

Предположительно, что  – дифференциальные функции в
– дифференциальные функции в  и ранг матрицы Якоби
и ранг матрицы Якоби 
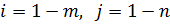 равен
равен 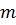 в каждойточке допустимой области
в каждойточке допустимой области  , определяемой условием
, определяемой условием  (3). Последнее означает, что градиенты
(3). Последнее означает, что градиенты  в точках
в точках  не обращается в нуль и линейно независимы, т.е. условия (3) задают зависимость
не обращается в нуль и линейно независимы, т.е. условия (3) задают зависимость 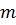 параметров
параметров  от
от  параметров. В этом случае:
параметров. В этом случае:
1. Вводится функция Лагранжа 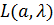
 ,
,
2. дальше 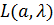 минимизируется как функция
минимизируется как функция  переменных
переменных  на безусловный минимум, т.е. используются необходимое и достаточные условия.
на безусловный минимум, т.е. используются необходимое и достаточные условия.
 Задача выпуклого программирования
Задача выпуклого программирования
 (1)
(1)
 (2)
(2)
где  и
и  - выпуклые дифференциальные функции.
- выпуклые дифференциальные функции.
Предположим, что допустимое множество  удовлетворяет условию регулярности (условие Слейтера):
удовлетворяет условию регулярности (условие Слейтера):
Существует точка  такая, что
такая, что  для всех
для всех  , т.е. существует у множества
, т.е. существует у множества  хотя бы одна внутренняя точка.
хотя бы одна внутренняя точка.
Говорят, что если в точке  выполняется неравенство
выполняется неравенство  , то это ограничение является пассивным в точке
, то это ограничение является пассивным в точке  . Очевидно, что для внутренней точки допустимого множества
. Очевидно, что для внутренней точки допустимого множества  все ограничения являются пассивными.
все ограничения являются пассивными.
Если же в точке  какое-то ограничение выполняется с равенством
какое-то ограничение выполняется с равенством  , то оно называется активным в точке
, то оно называется активным в точке  .
.
Обозначим через  множество индексов активных ограничений в точке
множество индексов активных ограничений в точке  .
.
 .
.
Введем дополнительные переменные  и перейдем от ограниченной – неравенств к ограниченным – равенствам
и перейдем от ограниченной – неравенств к ограниченным – равенствам
 (3)
(3)
функция Лагранжа для задачи (1), (3)
 (4)
(4)
И получим систему управлений для определения стационарных точек
 (5)
(5)
 (6)
(6)
 (7)
(7)
Условия (5), (6), (7) являются необходимыми условиями минимума в задаче (1), (3).
Исключим из этой системы вспомогательные переменные  .
.
Очевидно, условие (7) эквивалентно (2) (т.к. 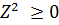 ).
).
Умножим каждое равенство (6) на  , тогда получим
, тогда получим
 или (с учетом (7))
или (с учетом (7))  . (8)
. (8)
Составим функцию Лагранжа задачи (1), (2)
 .
.
С учетом соотношения (5), (2) и (8) необходимые условия минимума в задаче (1) (2) принимают вид
 (9)
(9)
 (10)
(10)
 (11)
(11)
Условие (11) означает, что в искомой точке 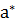 хотя бы один из сомножителей обращается в нуль.
хотя бы один из сомножителей обращается в нуль.
Если  , то
, то 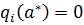 (ограничение с номером и является активным. Если же в точке
(ограничение с номером и является активным. Если же в точке 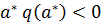 (пассивное ограничение), то
(пассивное ограничение), то  .
.
Условие (9) можно заменить
 (12)
(12)
Откуда следует, что антиградиент  в точке минимума является линейной комбинацией внешних нормалей к активным для точки
в точке минимума является линейной комбинацией внешних нормалей к активным для точки 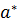 ограничениям.
ограничениям.
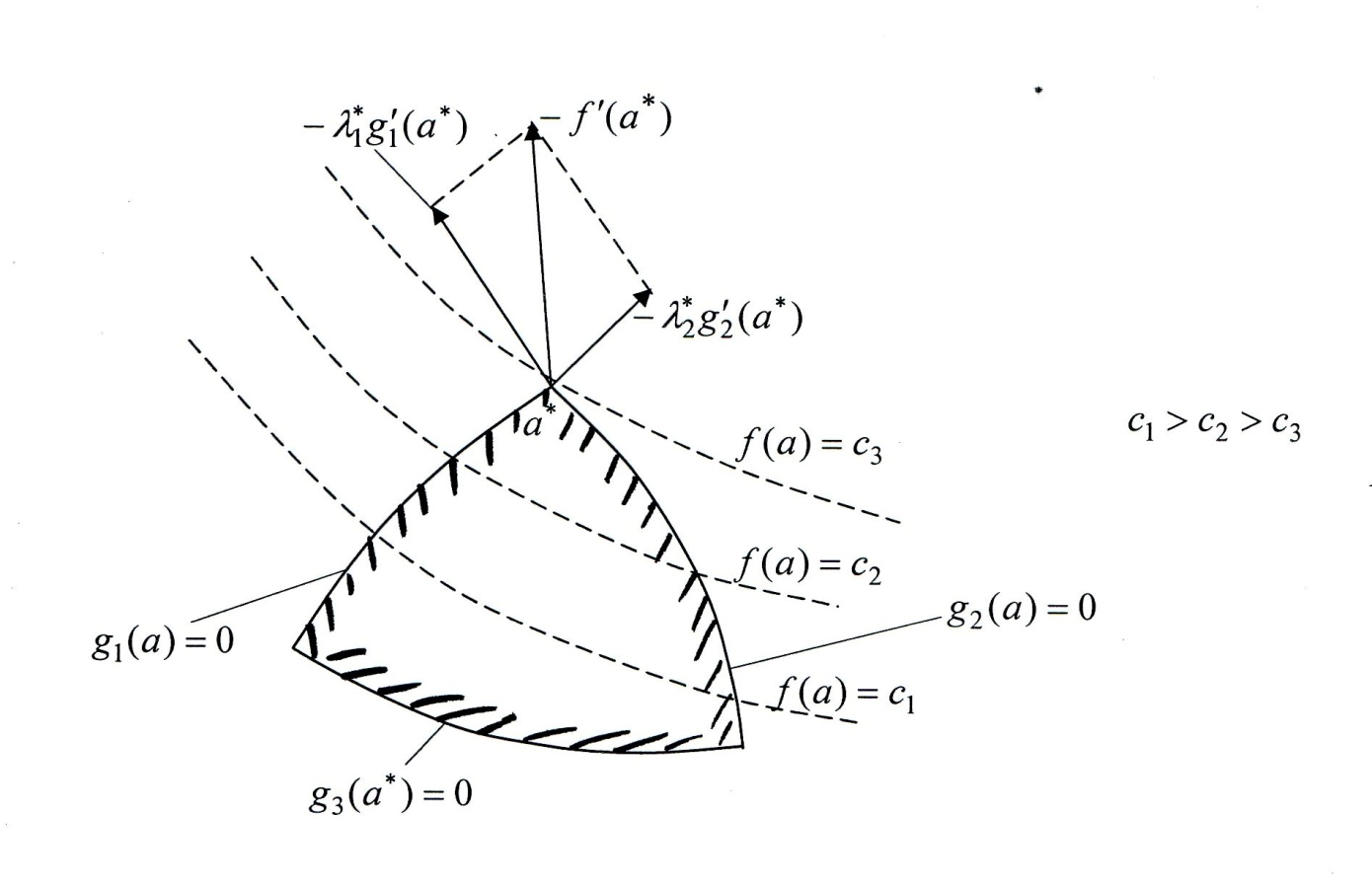
Тогда с учетом формул (9) – (11) можно сформулировать следующие необходимые условия минимума в задаче (1), (2) с допустимым множеством  , удовлетворяющим условию регулярности.
, удовлетворяющим условию регулярности.
Если 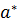 является решением задачи (1) (2), то для некоторых чисел
является решением задачи (1) (2), то для некоторых чисел
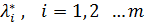 , выполняются соотношение
, выполняются соотношение
 (13)
(13)
 (14)
(14)
 (15)
(15)
 (16)
(16)
которые называются условиями Куна-Таккера.
Эти условия являются и достаточными условиями минимума в задаче (1), (2).
Теорема Куна-Таккера. Для того, чтобы 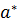 была решением задачи выпуклого программирования (1), (2) с дифференцируемыми функциями
была решением задачи выпуклого программирования (1), (2) с дифференцируемыми функциями 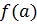 и
и  достаточно (
достаточно (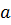 если
если  удовлетворяет условию регулярности, то и необходимая), чтобы существовал сектор
удовлетворяет условию регулярности, то и необходимая), чтобы существовал сектор  , для которого выполняются условия (13) – (16).
, для которого выполняются условия (13) – (16).
Задача математического программирования со смешанными ограничениями.
 (17)
(17)
 (18)
(18)
 (19)
(19)
 предполагаются дифференцируемыми.
предполагаются дифференцируемыми.
Справедлива следующая теорема Куна-Таккера:
Пусть в задаче (17) – (19) функции  выпуклы и дифференцируемы, функции
выпуклы и дифференцируемы, функции  – линейны, а допустимое множество
– линейны, а допустимое множество  удовлетворяет условию регулярности.
удовлетворяет условию регулярности.
Тогда, для того, чтобы 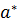 была решением задачи (17) – (19), необходимо и достаточно, чтобы существовали векторы
была решением задачи (17) – (19), необходимо и достаточно, чтобы существовали векторы 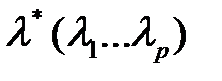 и
и 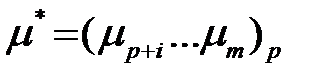 для которых выполняются условия:
для которых выполняются условия:
 (20)
(20)
 (21)
(21)
 (22)
(22)
 (23)
(23)
 (24)
(24)

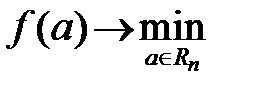

 – дифференциальные функции в
– дифференциальные функции в  и ранг матрицы Якоби
и ранг матрицы Якоби 
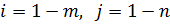 равен
равен 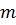 в каждойточке допустимой области
в каждойточке допустимой области  , определяемой условием
, определяемой условием  (3). Последнее означает, что градиенты
(3). Последнее означает, что градиенты  в точках
в точках  от
от  параметров. В этом случае:
параметров. В этом случае: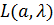
 ,
, переменных
переменных  на безусловный минимум, т.е. используются необходимое и достаточные условия.
на безусловный минимум, т.е. используются необходимое и достаточные условия. Задача выпуклого программирования
Задача выпуклого программирования (1)
(1) (2)
(2) и
и  - выпуклые дифференциальные функции.
- выпуклые дифференциальные функции. такая, что
такая, что  для всех
для всех  , т.е. существует у множества
, т.е. существует у множества  выполняется неравенство
выполняется неравенство  , то это ограничение является пассивным в точке
, то это ограничение является пассивным в точке  . Очевидно, что для внутренней точки допустимого множества
. Очевидно, что для внутренней точки допустимого множества  , то оно называется активным в точке
, то оно называется активным в точке  множество индексов активных ограничений в точке
множество индексов активных ограничений в точке  .
. и перейдем от ограниченной – неравенств к ограниченным – равенствам
и перейдем от ограниченной – неравенств к ограниченным – равенствам (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7) .
.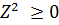 ).
). , тогда получим
, тогда получим или (с учетом (7))
или (с учетом (7))  . (8)
. (8) .
. (9)
(9) (10)
(10) (11)
(11)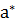 хотя бы один из сомножителей обращается в нуль.
хотя бы один из сомножителей обращается в нуль. , то
, то 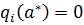 (ограничение с номером и является активным. Если же в точке
(ограничение с номером и является активным. Если же в точке 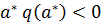 (пассивное ограничение), то
(пассивное ограничение), то  .
. (12)
(12) в точке минимума является линейной комбинацией внешних нормалей к активным для точки
в точке минимума является линейной комбинацией внешних нормалей к активным для точки 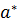 ограничениям.
ограничениям.
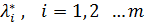 , выполняются соотношение
, выполняются соотношение (13)
(13) (14)
(14) (15)
(15) (16)
(16)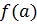 и
и  достаточно (
достаточно (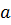 если
если  , для которого выполняются условия (13) – (16).
, для которого выполняются условия (13) – (16). (17)
(17) (18)
(18) (19)
(19) предполагаются дифференцируемыми.
предполагаются дифференцируемыми. выпуклы и дифференцируемы, функции
выпуклы и дифференцируемы, функции  – линейны, а допустимое множество
– линейны, а допустимое множество 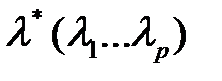 и
и 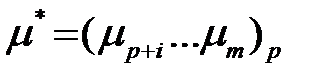 для которых выполняются условия:
для которых выполняются условия: (20)
(20) (21)
(21) (22)
(22) (23)
(23) (24)
(24)


