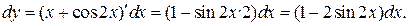Формулы дифференцирования основных элементарных функций
Замечание. Формулы записаны с учётом правила дифференцирования сложной функции. Производной n-го порядка называется производная от производной (n –1)-го порядка. Производные высших порядков вычисляются последовательным дифференцированием данной функции. Производная второго порядка Производная третьего порядка Задание 4. Найти производные функций: а) Решение. а) Используя правила I, III и формулу (3), получим:
б) Используя правила дифференцирования произведения функций II, разности I, формулы (5), (7), (8) и учитывая, что независимая переменная есть t, т. е. t ¢=1, получим:
в) Сложная степенная функция, независимая переменная есть v,
г) Используя правила дифференцирования частного IV, суммы I, III
Задание 5. Составить уравнение касательной и нормали к кривой Используем уравнения касательной (2) и нормали (3): 1) 2)
Подставим или
Задание 6. Найти дифференциалы функций: а) Для дифференциала функции Решение. а) б) в)
|



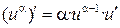

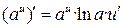

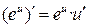


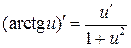



 или
или 
 или
или  и т. д.
и т. д.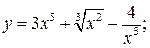 б)
б)  в)
в)  г)
г) 


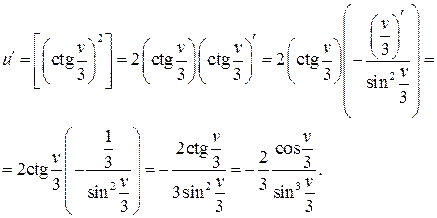

 в точке с абсциссой х 0=2.
в точке с абсциссой х 0=2.


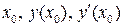 в уравнения и получим:
в уравнения и получим: 
 — уравнение касательной.
— уравнение касательной. или
или  — уравнение нормали.
— уравнение нормали. б)
б)  в)
в) 
 справедлива формула
справедлива формула  т. е. дифференциал функции равен произведению производной от функции на дифференциал независимой переменной.
т. е. дифференциал функции равен произведению производной от функции на дифференциал независимой переменной.