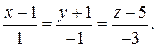Решим систему по формулам Крамера.
Найдём определитель системы, используя формулы (2) и (1):
Так как
Итак, Сделаем проверку, подставив найденные значения х 1, х 2, х 3 в исходную систему, и убедимся, что все три уравнения данной системы обращаются в тождества:
Ответ: х 1 = –1, х 2 = –1, х 3 =1. Элементы векторной алгебры в R 3 Трехмерное векторное пространство R 3 есть частный случай Rn при
Совокупность начала координат (точки О) и декартова прямоугольного базиса называется декартовой прямоугольной системой координат Oxyz. Согласно формуле (9) любой вектор
где ах — координата вектора по оси ОХ; ау — координата вектора по оси ОY; аz — координата вектора по оси ОZ.
А — начало вектора, В — конец вектора. Длина отрезка АВ называется модулем вектора и обозначается Если известны координаты вектора
Радиусом-вектором точки в декартовой прямоугольной системе координат называется вектор, начало которого расположено в начале координат, а конец в данной точке А, т. е. вектор Координатами точки А называются координаты её радиуса-вектора. Если Пусть вектор
Из (10) и (11) следует формула для расстояния между двумя точками А и В:
Скалярным произведением векторов
где j — угол между векторами В декартовой прямоугольной системе координат скалярное произведение векторов вычисляется по формуле:
Из (13) и (14) получается формула для вычисления косинуса угла между двумя векторами:
Векторы
Упорядоченная тройка векторов Векторным произведением вектора 1) 2) направлен так, что тройка 3) модуль вектора
Если
Смешанным произведением упорядоченной тройки векторов
Смешанное произведение векторов по абсолютной величине равно объему параллелепипеда
Если
Векторы 1) в векторной форме 2) в координатной форме Векторы 1) в векторной форме: 2) в координатной форме:
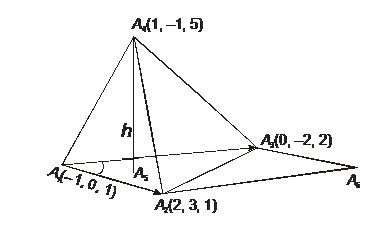
Требуется найти: а) длину ребра А 1 А 2; б) угол между ребрами А 1 А 2 и А 1 А 3;
а) Используем формулы (11) и (12). Определим координаты вектора:
Ребро б) Угол между рёбрами А 1 А 2 и А 1 А 3 рассматриваем как угол между векторами Найдём координаты и длину вектора
По формуле (15) для косинуса угла между двумя векторами получим:
в) Грань А 1 А 2 А 3 есть треугольник, площадь которого равна половине площади параллелограмма А 1 А 2 А 6 А 3, построенного на векторах Вычислим векторное произведение векторов
г) Объём треугольной пирамиды
Определим координаты вектора
По формуле (20) имеем
Элементы аналитической геометрии в R 3 Направляющим вектором прямой называется любой вектор
 , имеют вид: , имеют вид:
где (x, y, z) — координаты текущей точки прямой; (x 0, y 0, z 0) — координаты данной точки на прямой; (m, n, p) — координаты направляющего вектора прямой.
Рассматривая в качестве данной точки точку М 1 и используя уравнение (23), получим уравнения прямой, проходящей через две данные точки:
Пусть прямая l 1 имеет направляющий вектор Угол j между прямыми l 1 и l 2 определяется как угол между их направляющими векторами
Критерий перпендикулярности прямых
Уравнение плоскости, проходящей через данную точку М 0 плоскости и имеющей данный нормальный вектор
где А, В, С — координаты нормального вектора x 0, y 0, z 0 — координаты данной точки плоскости; x, y, z — координаты текущей точки плоскости. Если в уравнении (25) раскрыть скобки, то его можно записать в виде
Три точки М 1(x 1, y 1, z 1), М 2(x 2, y 2, z 2) и М 3(x 3, y 3, z 3) (не лежащие на одной прямой) определяют плоскость в R 3. Уравнение такой плоскости можно получить из условия компланарности (22) трёх векторов:
Здесь x, y, z — координаты текущей точки М; x 1, y 1, z 1 — координаты данной точки М 1; x 2, y 2, z 2 — координаты данной точки М 2; x 3, y 3, z 3 — координаты данной точки М 3.
Расстояние от точки М 0(x 0, y 0, z 0)
Угол между двумя плоскостями, нормальные векторы которых
Критерий параллельности плоскостей:
Критерий перпендикулярности плоскостей:
Угол между прямой и плоскостью ψ определяется как дополнительный к углу φ между направляющим вектором прямой
Пример 3 (продолжение). Даны координаты вершин треугольной пирамиды Требуется найти: д) канонические уравнения прямой А 1 А 4; е) уравнение плоскости А 1 А 2 А 3; ж) угол между ребром А 1 А 4 и гранью А 1 А 2 А 3; з) уравнение высоты, опущенной из вершины А 4 на грань А 1 А 2 А 3. Решение: д) Для нахождения канонических уравнений прямой А 1 А 4 используем уравнение (24) прямой, проходящей через две точки А 1 (–1, 0,1) и А 4 (1,–1, 5): А 1 А 4: е) уравнение плоскости А 1 А 2 А 3 получим, используя уравнение плоскости, проходящей через три данные точки А 1 (–1, 0, 1),
Раскладывая определитель по элементам первой строки, получим:
Делим все члены уравнения на 3 и раскрываем скобки:
Окончательно уравнение плоскости А 1 А 2 А 3 имеет вид:
ж) угол между ребром А 1 А 4 и гранью А 1 А 2 А 3 найдём как угол между прямой А 1 А 4 и плоскостью А 1 А 2 А 3 по формуле (29). Уравнение прямой получено в пункте д) и имеет вид Координаты направляющего вектора – это числа в знаменателях, следовательно: Используем формулу (29):
з) Уравнение высоты пирамиды получим как уравнение прямой А 4 А 5 (рис. 1). Поскольку высота перпендикулярна плоскости А 1 А 2 А 3, заданной уравнением
|


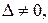 система имеет единственное решение, которое находим по формулам Крамера (5):
система имеет единственное решение, которое находим по формулам Крамера (5):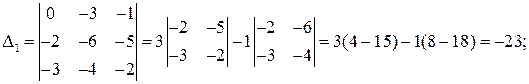




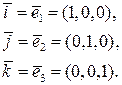
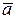 в R 3 можно разложить единственным образом по
в R 3 можно разложить единственным образом по  т. е. представить в виде:
т. е. представить в виде: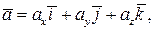
 Наряду с аналитическим заданием вектора как упорядоченной тройки чисел в R 3 рассматривают вектор как направленный отрезок, имеющий начало и конец. Конец вектора отмечается стрелкой.
Наряду с аналитическим заданием вектора как упорядоченной тройки чисел в R 3 рассматривают вектор как направленный отрезок, имеющий начало и конец. Конец вектора отмечается стрелкой.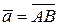
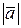 или
или  .
.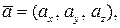 то модуль вектора вычисляется по формуле:
то модуль вектора вычисляется по формуле: (10)
(10)
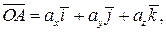 то
то 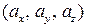 координаты точки А.
координаты точки А.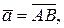 причём заданы координаты точек А и В:
причём заданы координаты точек А и В: 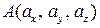 и
и  Тогда координаты вектора
Тогда координаты вектора  равны разности одноимённых координат конца и начала:
равны разности одноимённых координат конца и начала: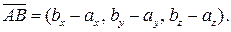 (11)
(11)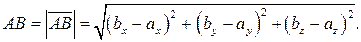 (12)
(12) называется число (скаляр), обозначаемое
называется число (скаляр), обозначаемое 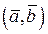 , равное произведению модулей векторов на косинус угла между ними:
, равное произведению модулей векторов на косинус угла между ними: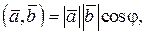 (13)
(13)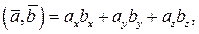 (14)
(14) — координаты вектора
— координаты вектора  (15)
(15)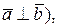 если угол j между ними равен прямому, т. е. cosj = 0. Условие ортогональности векторов:
если угол j между ними равен прямому, т. е. cosj = 0. Условие ортогональности векторов: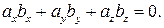 (16)
(16)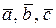 называется правой, если
называется правой, если 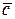 кратчайший поворот от первого вектора
кратчайший поворот от первого вектора 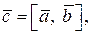 такой что:
такой что: т. е.
т. е. 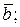
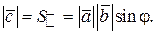 (17)
(17) то для векторного произведения справедлива формула:
то для векторного произведения справедлива формула: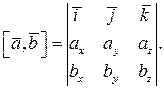 (18)
(18)
 , построенного на этих векторах как на сторонах, т. е.
, построенного на этих векторах как на сторонах, т. е.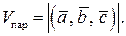 (19)
(19)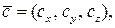 то справедлива формула:
то справедлива формула: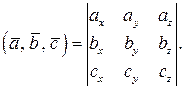 (20)
(20)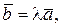 где l — скаляр;
где l — скаляр; (21)
(21)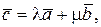 где l, m — числа;
где l, m — числа; (22)
(22) Пример 3. Даны координаты вершин треугольной пирамиды:
Пример 3. Даны координаты вершин треугольной пирамиды: 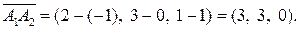
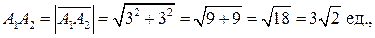
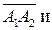

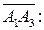
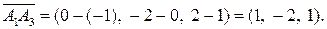
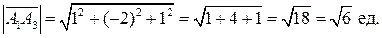

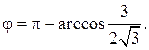
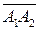
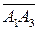 . По формуле (17):
. По формуле (17): 


 равен 1/6 объёма параллелепипеда
равен 1/6 объёма параллелепипеда  , построенного на векторах
, построенного на векторах  как на сторонах. Из свойств смешанного произведения следует, что:
как на сторонах. Из свойств смешанного произведения следует, что: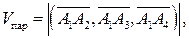 и следовательно,
и следовательно,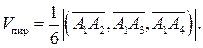
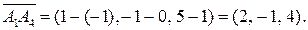

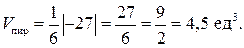
 и
и 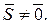
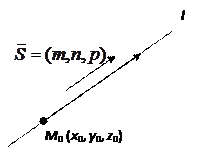
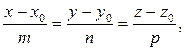 (23)
(23)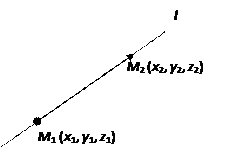 Если на прямой заданы две точки М 1(x 1, y 1, z 1) и М 2(x 2, y 2, z 2), то в качестве направляющего вектора прямой можно взять вектор
Если на прямой заданы две точки М 1(x 1, y 1, z 1) и М 2(x 2, y 2, z 2), то в качестве направляющего вектора прямой можно взять вектор 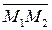 :
: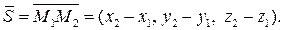
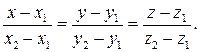 (24)
(24) и прямая l 2 — направляющий вектор
и прямая l 2 — направляющий вектор  .
.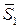 и
и 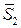 , по формуле (15) получаем:
, по формуле (15) получаем:
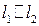 , если
, если 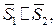 т. е. по условию коллинеарности (21)
т. е. по условию коллинеарности (21)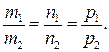
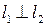 <=>
<=>  Тогда по условию ортогональности векторов (16)
Тогда по условию ортогональности векторов (16) 
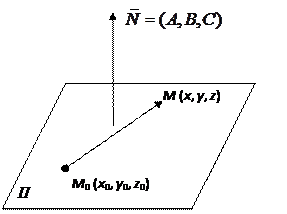 Нормальным вектором плоскости (П) называется любой вектор
Нормальным вектором плоскости (П) называется любой вектор  , перпендикулярный к плоскости и отличный от нуль-вектора:
, перпендикулярный к плоскости и отличный от нуль-вектора: 

 (25)
(25)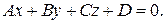 (26)
(26) Уравнение (26) называется общим уравнением плоскости.
Уравнение (26) называется общим уравнением плоскости.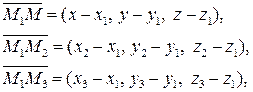
 (27)
(27) Пусть плоскость П задана общим уравнением
Пусть плоскость П задана общим уравнением 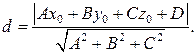 (28)
(28) и
и 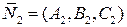 , вычисляется по формуле:
, вычисляется по формуле: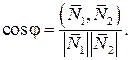

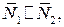
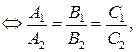
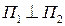
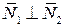
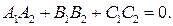
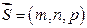 и вектором нормали к плоскости
и вектором нормали к плоскости 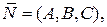 таким образомψ=900-φ и получаем:
таким образомψ=900-φ и получаем: . (29)
. (29) или
или 
 или
или 

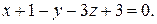
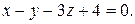
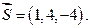 Уравнение плоскости получено в пункте е) и имеет вид
Уравнение плоскости получено в пункте е) и имеет вид  имеет координаты равные коэффициентам при х, у, z в уравнении плоскости, т. е.
имеет координаты равные коэффициентам при х, у, z в уравнении плоскости, т. е. 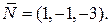
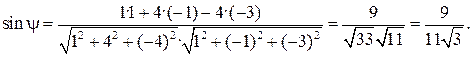
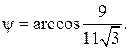
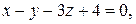 то вектор нормали к плоскости
то вектор нормали к плоскости 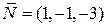 параллелен высоте и может быть использован в качестве направляющего вектора прямой А 4 А 5. Подставляя в формулу (23) координаты точки А 4 (1, –1, 5) и координаты направляющего вектора прямой
параллелен высоте и может быть использован в качестве направляющего вектора прямой А 4 А 5. Подставляя в формулу (23) координаты точки А 4 (1, –1, 5) и координаты направляющего вектора прямой  получим канонические уравнения прямой А 4 А 5:
получим канонические уравнения прямой А 4 А 5: