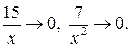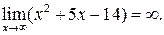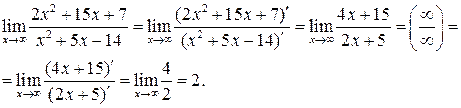Число А называют пределом функции f (x) при  (и пишут
(и пишут 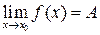 ), если для любого
), если для любого  найдется число
найдется число  зависящее от e, такое, что для всех
зависящее от e, такое, что для всех  , удовлетворяющих условию
, удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство 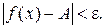
Функция a(x) называется бесконечно малой (б.м.ф.) при  (
( если
если 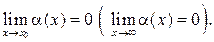
Функция f (x) называется бесконечно большой (б.б.ф.) при  , (
, ( если для любого M >0 найдётся число
если для любого M >0 найдётся число  зависящее от М, такое, что для всех
зависящее от М, такое, что для всех  , удовлетворяющих условию
, удовлетворяющих условию  , будет верно неравенство
, будет верно неравенство 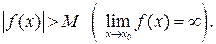
Если a(x) есть б. м.ф. при  (или
(или  то функция
то функция 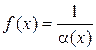
является б. б., и обратно, если f (x) б.б.ф. при  , то
, то 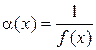 является б.м.ф.
является б.м.ф.
Если 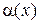 и
и  б.м.ф. при
б.м.ф. при  (
( ), то чтобы сравнить их, нужно вычислить предел их отношения. Пусть
), то чтобы сравнить их, нужно вычислить предел их отношения. Пусть 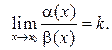 Тогда:
Тогда:
при  называется б.м. более высокого порядка малости, чем
называется б.м. более высокого порядка малости, чем  ;
;
при 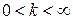
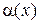 и
и  одного порядка малости;
одного порядка малости;
при 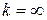
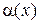 более низкого порядка малости, чем
более низкого порядка малости, чем  .
.
Если 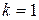 , то б.м.ф.
, то б.м.ф. 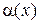 и
и  называются эквивалентными:
называются эквивалентными: 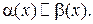
Предел отношения двух б.м.ф. не изменится, если каждую б.м.ф. заменить на эквивалентную.
Примеры эквивалентных б.м.ф. при 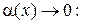
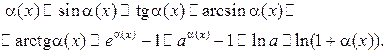
Теоремы о пределах:
1.  (c =const).
(c =const).
2. Если 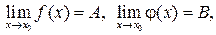 то:
то:
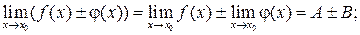
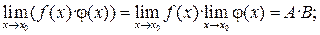
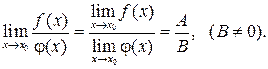
Первый замечательный предел: 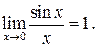
Второй замечательный предел (число е = 2,718…):
 или
или 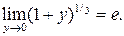
Чтобы найти предел элементарной функции 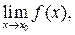 нужно предельное значение аргумента подставить в функцию и посчитать. При этом, если х = х 0 принадлежит области определения функции, то значение предела будет найдено, оно равно значению функции в точке х = х 0. При вычислении пределов полезно использовать следующие соотношения. Если
нужно предельное значение аргумента подставить в функцию и посчитать. При этом, если х = х 0 принадлежит области определения функции, то значение предела будет найдено, оно равно значению функции в точке х = х 0. При вычислении пределов полезно использовать следующие соотношения. Если 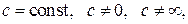 то, учитывая свойства б.б. и б.м. функций, получим:
то, учитывая свойства б.б. и б.м. функций, получим:
 если
если 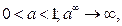 если a >1.
если a >1.
Случаи, в которых подстановка предельного значения аргумента
в функцию не дает значения предела, называют неопределенностями;
к ним относятся неопределенности видов:
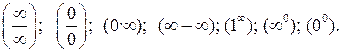
Устранить неопределенность можно с помощью алгебраических преобразований или используя правило Лопиталя.
Правило Лопиталя. Предел отношения двух б.м.  или б.б.
или б.б. 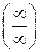 функций равен пределу отношения их производных (конечному или бесконечному), если последний существует:
функций равен пределу отношения их производных (конечному или бесконечному), если последний существует:
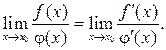 (5)
(5)
Чтобы использовать правило Лопиталя для раскрытия неопределённостей других типов, выражение под знаком предела следует преобразовать элементарными способами так, чтобы получить неопределенность  или
или 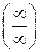 и затем использовать формулу (5).
и затем использовать формулу (5).
Задание 7. Найти пределы, используя правило Лопиталя или элементарные способы раскрытия неопределённостей:
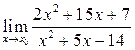 при а)
при а) 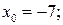 б)
б) 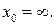
Решение.
а) 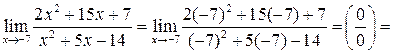
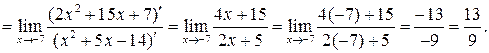
б) Подставляя в функцию вместо х предельное значение 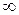 , определим предел числителя и знаменателя.
, определим предел числителя и знаменателя.
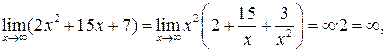 т. к.
т. к. 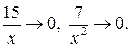
Аналогично: 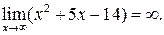
Имеем неопределенность вида 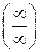 . Используем правило Лопиталя:
. Используем правило Лопиталя:
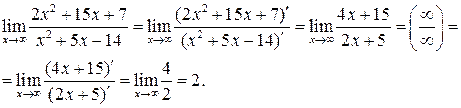
Замечание. Если, применив правило Лопиталя, снова получили неопределенность  или
или 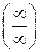 , то снова применяем правило до тех пор, пока неопределённость не будет раскрыта.
, то снова применяем правило до тех пор, пока неопределённость не будет раскрыта.

 (и пишут
(и пишут 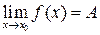 ), если для любого
), если для любого  найдется число
найдется число  зависящее от e, такое, что для всех
зависящее от e, такое, что для всех  , удовлетворяющих условию
, удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство 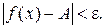
 если
если 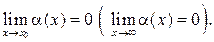
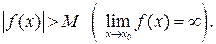
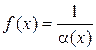
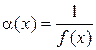 является б.м.ф.
является б.м.ф.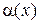 и
и  б.м.ф. при
б.м.ф. при  ), то чтобы сравнить их, нужно вычислить предел их отношения. Пусть
), то чтобы сравнить их, нужно вычислить предел их отношения. Пусть 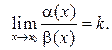 Тогда:
Тогда: называется б.м. более высокого порядка малости, чем
называется б.м. более высокого порядка малости, чем 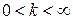
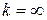
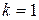 , то б.м.ф.
, то б.м.ф. 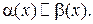
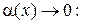
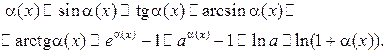
 (c =const).
(c =const).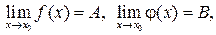 то:
то: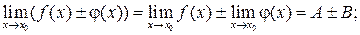
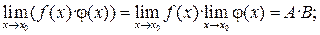
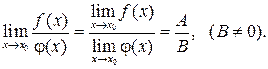
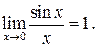
 или
или 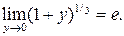
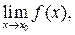 нужно предельное значение аргумента подставить в функцию и посчитать. При этом, если х = х 0 принадлежит области определения функции, то значение предела будет найдено, оно равно значению функции в точке х = х 0. При вычислении пределов полезно использовать следующие соотношения. Если
нужно предельное значение аргумента подставить в функцию и посчитать. При этом, если х = х 0 принадлежит области определения функции, то значение предела будет найдено, оно равно значению функции в точке х = х 0. При вычислении пределов полезно использовать следующие соотношения. Если 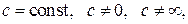 то, учитывая свойства б.б. и б.м. функций, получим:
то, учитывая свойства б.б. и б.м. функций, получим: если
если 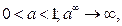 если a >1.
если a >1.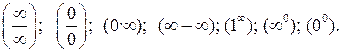
 или б.б.
или б.б. 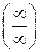 функций равен пределу отношения их производных (конечному или бесконечному), если последний существует:
функций равен пределу отношения их производных (конечному или бесконечному), если последний существует: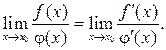 (5)
(5)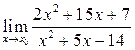 при а)
при а) 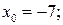 б)
б) 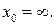
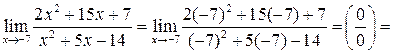
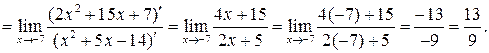
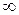 , определим предел числителя и знаменателя.
, определим предел числителя и знаменателя.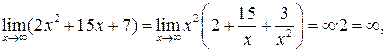 т. к.
т. к.