КВАНТОВАЯ ОПТИКА И АТОМНАЯ ФИЗИКА
1. Максимум энергии излучения абсолютно черного тела приходится на длину волны 450 нм. Определить температуру и энергетическую светимость тела. Дано: λmaх = 450 нм = 4,5·10-7 м; b = 2,89·10-3 м·К; σ = 5,67·10-8 Вт/(м2·К4). Найти: Т, R. Решение. Длина волны λmax, на которую приходится максимум энергии излучения черного тела, по закону Вина равна: λmax = Отсюда: В соответствии с законом Стефана - Больцмана энергетическая светимость R абсолютно черного тела равна: R = σT4. В результате вычислений имеем:
2. Красная граница фотоэффекта для никеля равна 0,257 мкм. Найти длину волны света, падающего на никелевый электрод, если фототок прекращается при задерживающей разности потенциалов, равной 1,5 В. Дано: λк= Найти: λ. Решение. Согласно уравнению Эйнштейна для внешнего фотоэффекта:
Красная граница фотоэффекта определяется из условия равенства энергии фотона
Максимальная кинетическая энергия фотоэлектронов может быть определена через задерживающую разность потенциалов Uз: Екmax= eU3, (3) где е – заряд электрона. Подставляя выражения (2) и (3) в (1), получим:
Из уравнения (4) найдем длину волны света:
Подставляя в (5) числовые значения, получим:
3. Определить максимальную скорость электрона, вырванного с поверхности металла γ – квантом с энергией 1,53 МэВ. Дано: Е = 1,53 МэВ; Е0 = 0,511 МэВ (энергия покоя электрона). Найти: vmax, Решение: По формуле Эйнштейна для фотоэффекта: Е = Авых+Ек.max.. Энергия кванта излучения расходуется на работу вырывания электрона Авых и сообщение ему кинетической энергии Ек.max.. Так как Авых<< Е, то электрон будет релятивистским и Е
где Е0 – энергия покоя электрона.
4. Гамма-фотон с длиной волны 1,2 пм в результате комптоновского рассеяния на свободном электроне отклонился от первоначального направления на угол 600. Определить кинетическую энергию и импульс электрона отдачи. До столкновения электрон покоился. Дано: Найти: Ек, р. Решение. Изменение длины волны фотона при комптоновском рассеянии на неподвижном свободном электроне равно:
где λ1 и λ2 – длины волн падающего и рассеянного фотона, θ – угол рассеяния фотона, Из выражения (1) найдем: Выразим энергию падающего и рассеянного фотона через его длину волны:
Кинетическая энергия электрона отдачи согласно закону сохранения энергии равна: Подставляя выражения (3) в (4), найдем:
Сделав вычисления, получим:
Подставляя в (6) числовые данные, получим:
5. Сколько линий спектра атома водорода попадает в видимую область света Дано: Найти: λ. Решение: Длины волн спектра атома водорода определяются по формуле:
Квантом излучения в видимой области спектра соответствуют переходы электронов на второй энергетический уровень (n = 2). Перебирая возможные варианты, находим, что в видимой области спектра находятся первые четыре линии серии Бальмера (n = 2; k = 3, 4, 5, 6). Длины волн этих линий будут равны:
6. Определить кинетическую энергию протона и электрона, для которых длина волны де Бройля равна 0,06 нм. Дано: Найти: Ее, Ер. Решение. Длина волны де Бройля Тогда импульс частицы равен: Подставив эти выражения в формулу для энергии, получим: Тогда для электрона: Для протона:
7. В атоме среднее время жизни электронов в возбужденном состоянии составляет 10 нс. Вычислить естественную ширину спектральной линии (λ = 0,7 мкм), соответствующей переходу между возбужденными уровнями атома. Дано: τ = 10-8 с; λ = 7·10-7 м. Найти: Δλmin. Решение. При переходе электрона из одного стационарного состояния в другое излучается (или поглощается) квант энергии, равный:
Из (1) следует, что неопределенность длины волны Δλ излучения, определяющая естественную ширину спектральной линии, связана с неопределенностью энергии уровней электронов в атоме ΔΕn и ΔΕk соотношением:
Согласно соотношению неопределенностей Гейзенберга:
где Δt – неопределенность времени перехода атома из одного стационарного состояния в другое. Поскольку Δt не превышает среднее время жизни τ возбужденного состояния атома, то минимальная неопределенность энергии возбужденных уровней, согласно (3), равна:
Из (2) с учетом (4) найдем минимальную неопределенность длины волны излучения, которая называется естественной шириной спектральной линии:
Если одно из состояний, между которыми совершается переход, является основным, то
поскольку для основного состояния tn = ¥. Для возбужденных состояний с одинаковым временем жизни τn = τk = τ имеем:
Подставляя в (7) числовые значения, получим:
8. Кинетическая энергия электрона в атоме водорода порядка 10 эВ. Используя соотношение неопределенностей, оценить минимальные линейные размеры атома. Дано: Е = 10 эВ = 1,6·10-18 Дж; m = 9,1·10-31 кг. Найти: r. Решение. Минимальные размеры атома можно оценить, исходя из соотношения неопределенностей Гейзенберга: Δх×Δpх ≥ ћ, где Δх – неопределенность координаты, Δрх – неопределенность импульса, ћ = h/2p – постоянная Планка. Предполагая, что Δх ≈ r – соответствует линейному размеру атома, получим
Предполагая, что по порядку величина Δр ≈ р, оценим r:
9. Электрон находится в одномерной потенциальной яме с бесконечно высокими стенками. Ширина ямы l = 1 нм. Определить наименьшую разность энергетических уровней электрона. Дано: l = 10-9 м, m = 9,1×10-31 кг, h = 6,64×10-34 Дж×с. Найти: ΔЕmin. Решение. Энергия электрона Еn, находящегося в потенциальной яме шириной l, на n-м энергетическом уровне определяется по формуле:
Разность ΔΕn,n+1 энергий электрона на соседних n и (n+1)-м уровнях равна:
Очевидно, что ΔΕ будет минимальна при n = 1. Тогда:
10. Вычислить дефект массы, энергию связи и удельную энергию связи ядра Дано: m Z = 8; А = 16. Найти: Δm, Есв, εсв. Решение. Дефект массы Δm ядра определяется по формуле: Δm = Zmp + (A-Z)mn - mя. (1) В таблицах чаще всего приводят массу атомов (изотопов), т.е. суммарную массу ядра вместе с электронами, то формулу (1) можно записать также в виде: Δm = Zm где ma-масса изотопа, дефект массы ядра которого необходимо определить. Подставляя в (2) числовые данные, получим: Δm = 0,13708 а.е.м. Энергия связи ядра Есв определяется по формуле: Есв = с2Δm. (3) Если дефект массы Δm выражать в а.е.м., а энергию связи Есв в МэВ, то формула (3) примет вид: Есв = 931 Δm (МэВ). (4) Подставляя в (4) числовые значения, получим: Есв = 931·0,13708 ≈ 128 (МэВ). Удельная энергия связи εсв вычисляется по формуле: εсв= Проведя вычисления, получим: εсв =
11. За год распалось 60 % атомов некоторого радиоактивного элемента. Определить период полураспада этого элемента. Дано: t = 1 год; Найти: T1/2. Решение. Закон радиоактивного распада имеет вид: N = N0·e-λt, где N0 – исходное число радиоактивных ядер, N – число не распавшихся ядер через время t, λ - постоянная радиоактивного распада, которая связана с периодом полураспада T1/2 соотношением: T1/2 =
е-λt = 0,4; еλt = Тогда: T1/2 =
12. Вычислить энергию ядерной реакции: Решение. Энергия ядерной реакции определяется по формуле: Q = c2(m1 + m2 - ∑mi), (1) где m1 и m2 - массы ядер и частиц, вступающих в ядерную реакцию, ∑mi - сумма масс ядер и частиц, образовавшихся в результате реакции. Если массу частиц выражать в а.е.м., а энергию реакции в МэВ, то формула (1) примет вид: Q = 931(m1 + m2 - ∑mi). (2) При вычислении энергии ядерной реакции можно использовать массы атомов вместо масс их ядер. Из справочных данных находим:
Дефект массы реакции равен: Dm = (2 Подставляя значение дефекта массы реакции в (2), получим: Q = 931(-0,01864) ≈ -17,4 (МэВ).
|

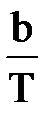 .
.
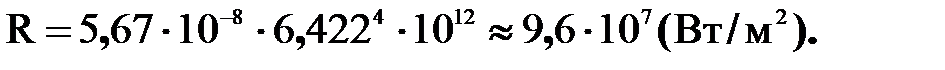
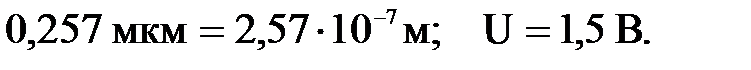
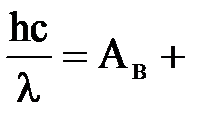 Екmax. (1)
Екmax. (1)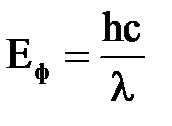 работе выхода электронов АВ, т. е.
работе выхода электронов АВ, т. е. . (2)
. (2)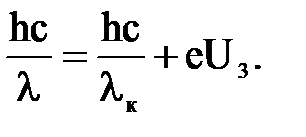 (4)
(4) (5)
(5)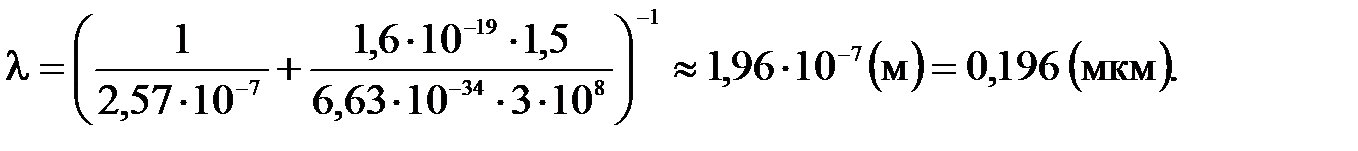
 Ек, а кинетическая энергия будет выражаться формулой:
Ек, а кинетическая энергия будет выражаться формулой: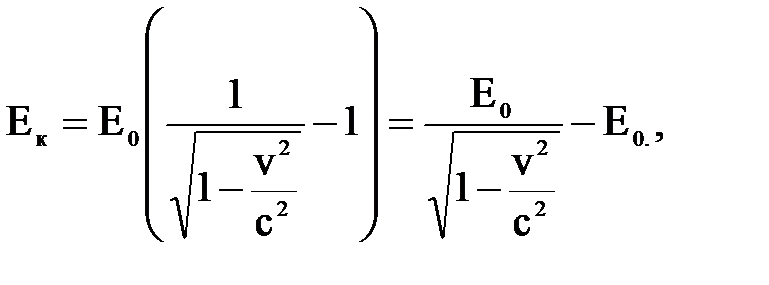

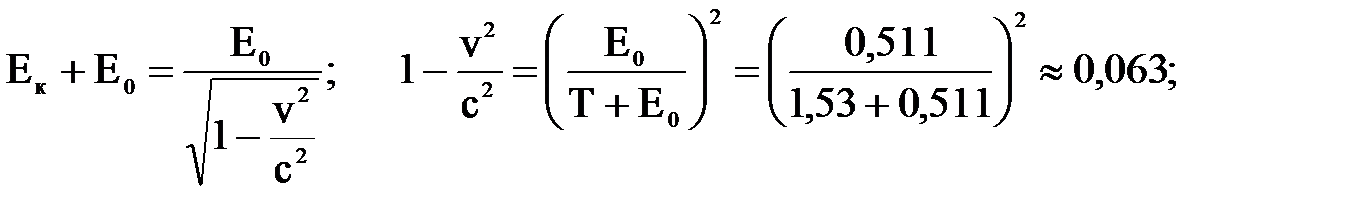
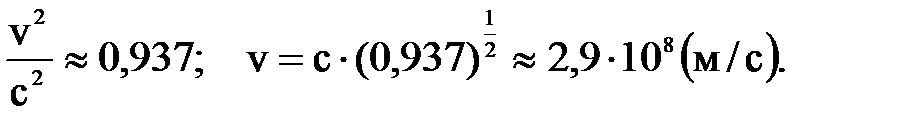
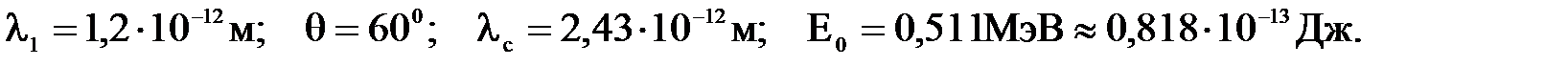
 (1)
(1)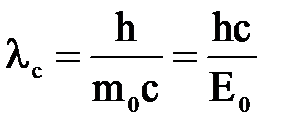 - комптоновская длина волны электрона.
- комптоновская длина волны электрона.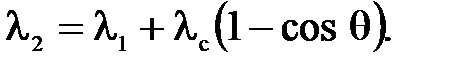 (2)
(2)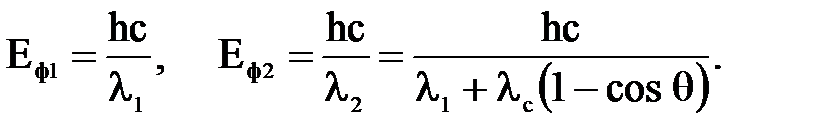 (3)
(3) (4)
(4)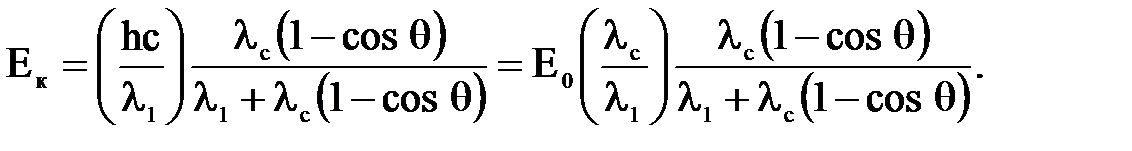 (5)
(5)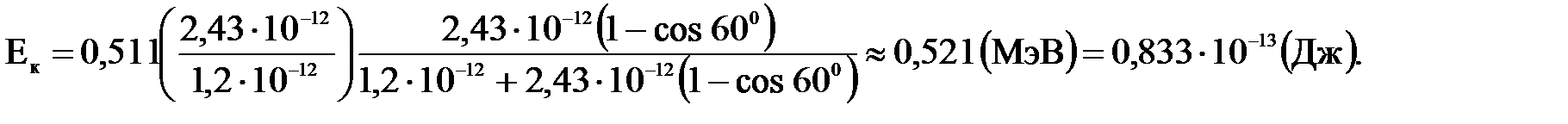 Зная кинетическую энергию электрона, найдем его импульс. Поскольку кинетическая энергия электрона сравнима с его энергией покоя, то импульс и кинетическая энергия связаны соотношением:
Зная кинетическую энергию электрона, найдем его импульс. Поскольку кинетическая энергия электрона сравнима с его энергией покоя, то импульс и кинетическая энергия связаны соотношением: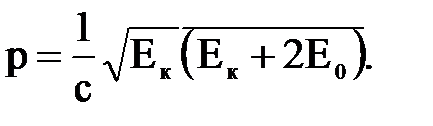 (6)
(6)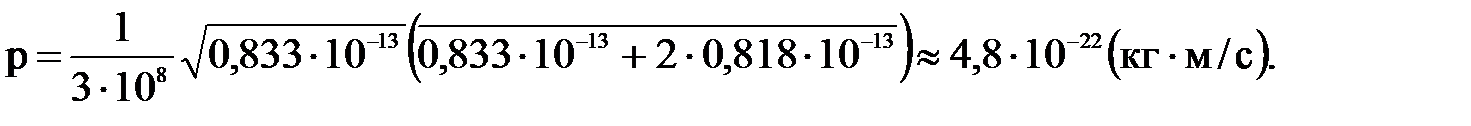
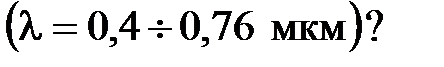 Вычислить длину волн этих линий. Каким цветам они соответствуют?
Вычислить длину волн этих линий. Каким цветам они соответствуют?
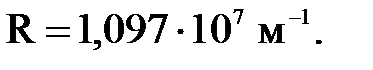
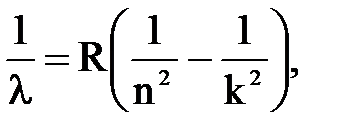 где n = 1, 2, 3,...,k = n + 1; n + 2;....
где n = 1, 2, 3,...,k = n + 1; n + 2;....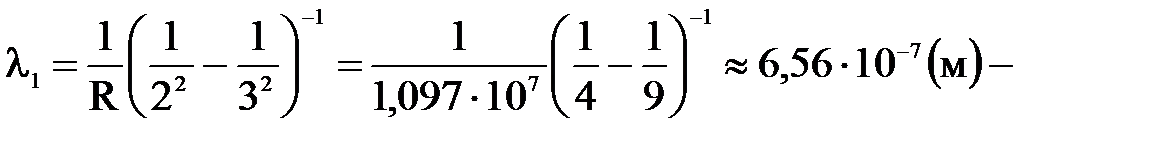 красная линия;
красная линия;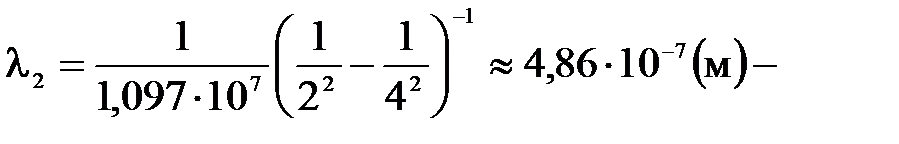 голубая линия;
голубая линия;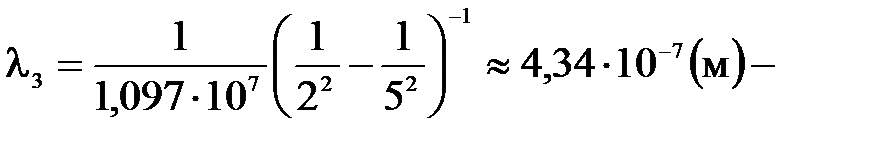 фиолетовая линия;
фиолетовая линия;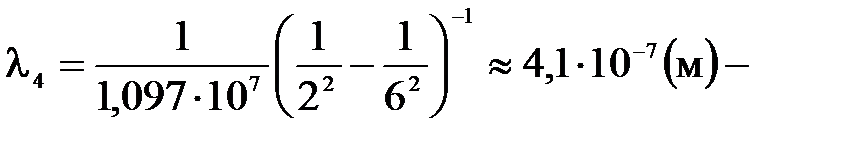 фиолетовая линия.
фиолетовая линия.
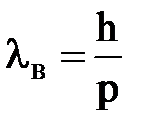 . Из уравнения кинетической энергии движущейся частицы следует:
. Из уравнения кинетической энергии движущейся частицы следует: 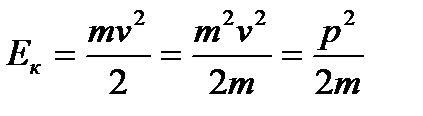 .
.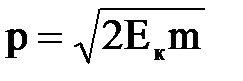 , а
, а 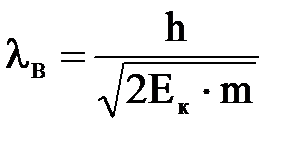 .
.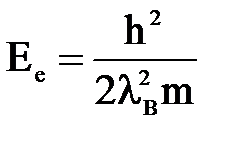 .
.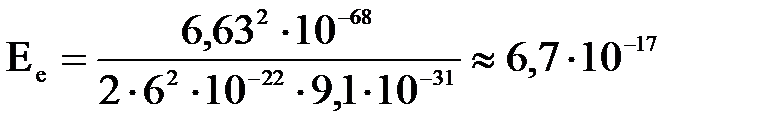 (Дж) = 419 (эВ).
(Дж) = 419 (эВ).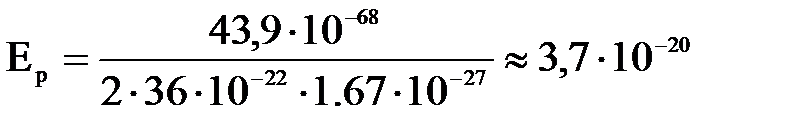 (Дж) ≈ 0,23(эВ).
(Дж) ≈ 0,23(эВ).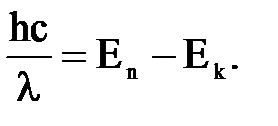 (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5)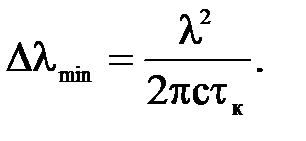 (6)
(6)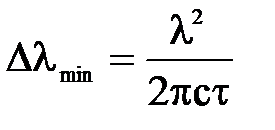 . (7)
. (7) (м).
(м).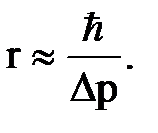 Импульс электрона, обладающего кинетической энергией Е, равен:
Импульс электрона, обладающего кинетической энергией Е, равен: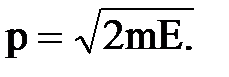
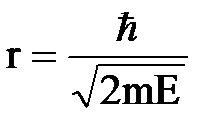 ;
; 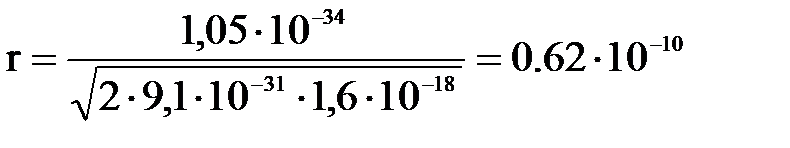 (м).
(м).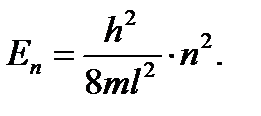
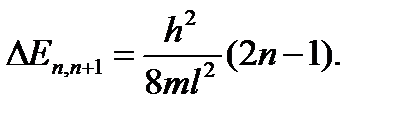
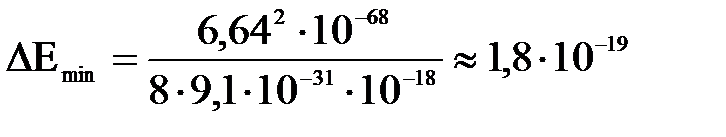 (Дж) ≈ 1,1 (эВ).
(Дж) ≈ 1,1 (эВ).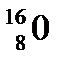 .
.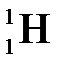 = 1.00783 а.е.м.; mn = 1,00867 а.е.м.; m
= 1.00783 а.е.м.; mn = 1,00867 а.е.м.; m 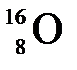 = 15,99492 а.е.м.;
= 15,99492 а.е.м.;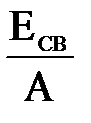 . (5)
. (5) = 8 (МэВ).
= 8 (МэВ).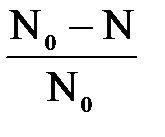 = 0,6.
= 0,6.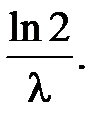 . По условию задачи:
. По условию задачи: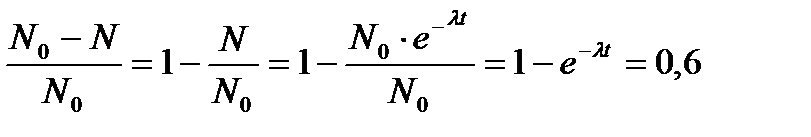 ;
;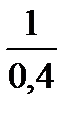 = 2,5; λt = ln 2,5; λ =
= 2,5; λt = ln 2,5; λ = 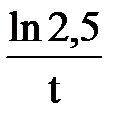 .
.
 Выделяется или поглощается энергия при этой реакции?
Выделяется или поглощается энергия при этой реакции?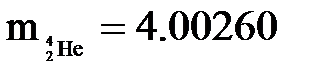 а.е.м.,
а.е.м., 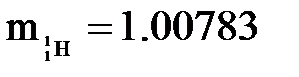 а.е.м.,
а.е.м., 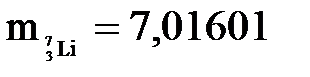 а.е.м.
а.е.м.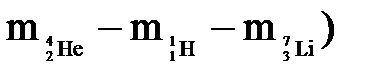 = - 0,01864 а.е.м.
= - 0,01864 а.е.м.


