Решение. По закону Ома для замкнутой цепи: .
При коротком замыкании цепи внешнее сопротивление R = 0 и
6. К источнику тока подключают один раз резистор сопротивлением 1 Ом, другой раз — 4 Ом. В обоих случаях на резисторах за одно и то же время выделяется одинаковое количество теплоты. Определить внутреннее сопротивление источника тока. Дано: R 1= 1 Ом; R 2= 4 Ом; t 1 = t 2 = t, Q l = Q 2. Найти: r. Решение. По закону Ома, По закону Джоуля - Ленца, количество теплоты Q, выделяемое в проводнике при прохождении тока за время t, равно: Так как После математических преобразований получим:
7. Сила тока в резисторе линейно возрастает за 4 с от 0 до 8 А. Сопротивление резистора 10 Ом. Определить количество теплоты, выделившееся в резисторе за первые 3 с. Дано: t 0 = 0; t 1= 4 с; I = 0; 1 1 = 8 A; t 2= 3 с; R = 10 Ом. Найти: Q. Решение. По закону Джоуля – Ленца: Так как сила тока является функцией времени, то где k — коэффициент пропорциональности, численно равный приращению тока в единицу времени: Следовательно, За первые 3 с выделится количество теплоты, равное
Подставляя числовые значения, получим:
8. Батарея состоит из пяти последовательно соединенных элементов. ЭДС каждого 1,4 В, внутреннее сопротивление 0,3 Ом. При каком токе полезная мощность батареи равна 8 Вт? Определить наибольшую полезную мощность батареи. Дано: εi = 1,4 В; ri = 0,3 Ом; Р п = 8 Вт; п = 5. Найти: I, Р п mах. Решение. Полезная мощность батареи Сила тока определяется по закону Ома: Здесь Выразим R из (1):
или Преобразуя выражение (4), получим квадратное уравнение относительно I:
Решая квадратное уравнение, найдем: Подставляя числовые значения, получим:
Для того чтобы определить наибольшую полезную мощность батареи, найдем зависимость её от внешнего сопротивления. Подставим в уравнение (1) выражение (2): Из этой формулы следует, что при постоянных величинах εi и ri мощность является функцией одной переменной — внешнего сопротивления R. Известно, что эта функция имеет максимум, если
или Таким образом, задача сводится к отысканию сопротивления внешней цепи. Из решения уравнения (6) следует, что Производя вычисления, найдем:
9. Найти значения сил токов на различных участках схемы. Заданы ЭДС источников ε1 = 1 В, ε2 = 3 В и сопротивления R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом. Внутренние сопротивления источников не учитывать. Дано: ε1 = 1 В, ε2 = 3 В, R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом. Найти: I1, I2, I3.
Рисунок 5 Также произвольно выберем направления обходов контуров, в данном случае – по часовой стрелке. Запишем первое правило Кирхгофа применительно к узлу А: I1 - I2 + I3 = 0. (1) Выберем контуры ε1 – A – R3 – B – R1 – ε1, ε2 – A – R3 – B – R2 – ε2 и запишем для них соответственно второе правило Кирхгофа:
Получаем систему трёх уравнений с тремя неизвестными. Решая её, получаем:
Отрицательные значения токов означают, что эти токи в действительности направлены противоположно показанному на рисунке 5. Находим I1:
10. Источники тока с электродвижущими силами 10 В и 4 В включены в цепь, как показано на рисунке. Определить силы токов, текущих через второе и третье сопротивления, если R1 = R4 = 2 Ом и R2 = R3 = 4 Ом. Сопротивлением источников тока пренебречь. Дано: ε1 = 10 В; ε2 = 4 В; R1= R4 = 2 Ом; R2 = R3 = 4 Ом. Найти: I1; I2; I3. Решение:
Рисунок 6 По первому правилу Кирхгофа для узла В имеем:
По второму правилу Кирхгофа имеем соответственно для контуров AR1BR2A, AR1BR3A, AR3BR4A (см. рис. 6):
Для решения воспользуемся методом Крамера. Для этого в равенства (2) – (4) подставим значения сопротивлений и эдс и уравнения перепишем в следующем виде:
Искомые значения токов найдем из выражений:
Получим, что I2 = 0, I3 = -1 A. Знак ” - “ у значения силы третьего тока свидетельствует о том, что при произвольном выборе направления токов, указанных на рисунке, направление тока было указано противоположно истинному. Третий ток течет от узла В к узлу А.
|

 , откуда
, откуда  . Тогда
. Тогда  или
или  .
. .
. .
. , то
, то  , тогда
, тогда  ;
; ;
; ;
;  ;
;  ;
; ;
;  .
. . (1)
. (1) , (2)
, (2) .
. . (3)
. (3) . (4)
. (4) .
. . (1)
. (1)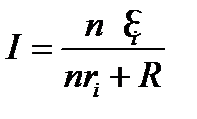 . (2)
. (2) — ЭДС, а
— ЭДС, а  — внутреннее сопротивление п последовательно соединенных элементов.
— внутреннее сопротивление п последовательно соединенных элементов. и, подставив это выражение в (2), получим
и, подставив это выражение в (2), получим (3)
(3) . (4)
. (4) .
. .
. ;
; .
. . (5)
. (5) , следовательно, имеем:
, следовательно, имеем: ,
, . (6)
. (6) .Подставляя найденное значение R в формулу (5), имеем:
.Подставляя найденное значение R в формулу (5), имеем:  .
. .
. ,
,  . (2)
. (2) А,
А, А.
А. A.
A.
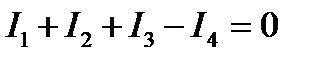 . (1)
. (1) (2)
(2)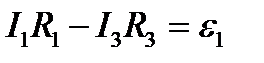 (3)
(3) (4)
(4) ;
;  ;
; 
 ;
;  .
.


