Приклади розв’язання задач
Задача 1. Знайти швидкість човна відносно берега річки, який пливе під кутом a=30° до течії, якщо швидкість течії річки v 1=1,5 м/с, швидкість човна відносно води v 2=2,5 м/с. Дано: a = 30° v 1=1,5 м/с v 2=2,5 м/с
Розв’язок: Швидкість човна відносно берега є векторною сумою швидкостей За теоремою косинусів знайдемо модуль вектора швидкості v 2 = v 12 + v 22 – 2 v 1 v 2 cos (p – a);
Показаний на рис. 1.4 кут b визначає напрямок вектора швидкості
Відповідь: Задача 2. Вільно падаюче тіло за останні 2 с польоту пройшло 196 м шляху. З якої висоти воно впало? Дано: Dt=t2 – t1 = 2 c s = 196 м h –? Рис. 1.5 Нехай у момент часу t=0 c координата y тіла дорівнює y = h метрів, а в моменти часу t= t1 c і t= t2 c – y = s м і y = 0 м відповідно (див. рис. 1.5). Рух тіла відбувається у полі тяжіння Землі, тому прискорення тіла – це прискорення вільного падіння g =9,8 м/с2. Кінематична формула залежності координати y від часу
За умовою задачі початкова координата y0 = h м, початкова швидкість v 0 = 0 м/с, прискорення h, t1 і t2 , розв’язавши яку, знайдемо відповідь задачі:
Відповідь: Задача 3. На висоті 10 м над Землею кинуто камінь під кутом 30° до горизонту зі швидкістю v =20 м/с. Знайти найбільшу висоту каменя над поверхнею Землі під час його польоту і відстань, яку він здолає у горизонтальному напрямку. Опором повітря знехтувати. Дано: h = 10 м v 0=20 м/с a = 30° H –? s –? Розв’язок: Рис. 1.6 Рух тіла відбувається у полі тяжіння Землі, тому прискорення тіла – це прискорення вільного падіння g =9,8 м/с2. Розкладемо рух каменя на два компоненти: 1) рівномірний рух уздовж осі x; 2) рівноприскорений рух уздовж осі y. Кінематичні формули залежності координат x і y від часу, а також відповідних швидкостей v x i v y такі:
За умовою задачі: початкові координати – y0 = h м, x0 = 0 м; початкові швидкості – v 0x = v 0 cos a м/с, v 0x = v 0 sin a м/с; прискорення –
У верхній точці D v y = 0 м/с. Отже з останньої формули можна знайти момент часу, коли камінь має найбільшу висоту:
і за формулою (1.7) саму цю висоту:
Момент часу tп падіння знайдемо з рівняння
Час завжди додатній, тому перший корінь відкидаємо і за формулою (1.6) обчислимо шлях у горизонтальному напрямі s:
Відповідь: Задача 4. Шлях s, який проходить матеріальна точка вздовж кола радіусом 4 м, від часу залежить за законом s=A+Bt+Ct2, де A =2 м, В =3 м/с, С=1 м/с2. Знайти прискорення а точки у момент часу і сам момент часу, коли нормальне прискорення дорівнює 4 м/с2. Дано: R=4 м s=A+Bt+Ct2 A =2 м В = 3 м/с С=1 м/с2 an=4 м/с2 v –? a –? Розв’язок: Знайдемо формули для швидкості й тангенціального прискорення. Для цього продиференцюємо вираз для s:
Можемо визначити прискорення а за теоремою Піфагора (див. рис. 1.7): Рис. 1.7
Потрібний момент часу знайдемо з умови an=4 м/с2. Скориставшись формулою для нормального прискорення
отримаємо два значення моменту часу: t1=0,5 c і t2= Друге значення часу відкидаємо, бо воно не задовольняє умові задачі (t³0). Відповідь:
|

 –?
–? :
:  (див. рис. 1.4).
(див. рис. 1.4). :
:
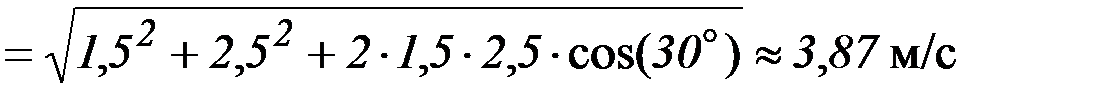 .
. ,
, .
.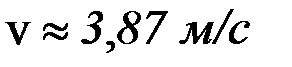 ,
,  .
. . (1.1)
. (1.1) м/с2. Записавши формулу (1.1) для моментів часу t= t1 c і t= t2 c, а також вираз з умови t2 – t1 = 2 c, отримаємо систему трьох алгебраїчних рівнянь з трьома невідомими
м/с2. Записавши формулу (1.1) для моментів часу t= t1 c і t= t2 c, а також вираз з умови t2 – t1 = 2 c, отримаємо систему трьох алгебраїчних рівнянь з трьома невідомими





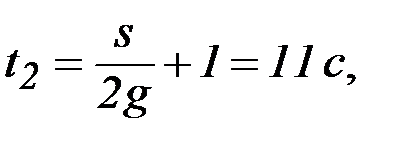
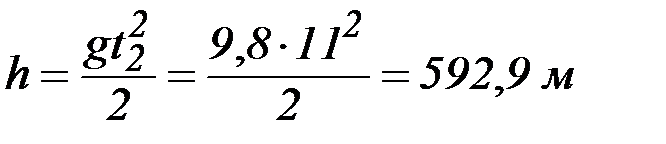 .
. .
. (1.2)
(1.2) (1.3)
(1.3) (1.4)
(1.4) . (1.5)
. (1.5) м/с2,
м/с2,  м/с2. З урахуванням цього формули (1.2)–(1.5) перепишемо у вигляді
м/с2. З урахуванням цього формули (1.2)–(1.5) перепишемо у вигляді (1.6)
(1.6) (1.7)
(1.7)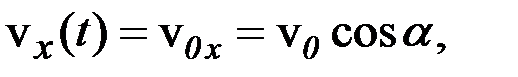 (1.8)
(1.8)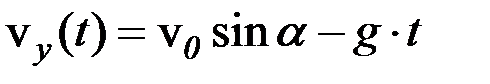 . (1.9)
. (1.9) ;
;  ;
;  ;
;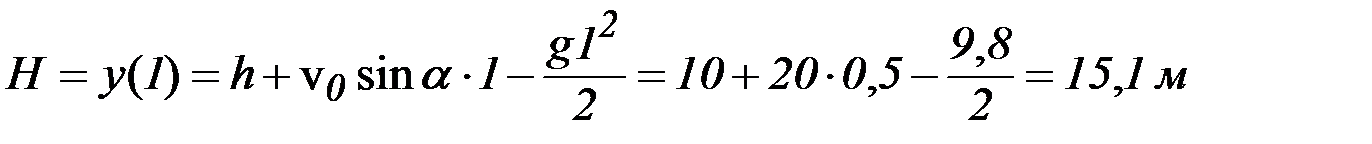 .
. .
. ;
;  ;
; ;
;  .
. .
.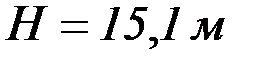 ,
,  .
. s=B+2Ct=3+2t,
s=B+2Ct=3+2t, =2C=2 м/с2.
=2C=2 м/с2. .
. ,
,  ,
,  ,
, c.
c. , t=0,5 c.
, t=0,5 c.


