1. Найти общее и особое решения автономного уравнения
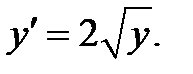
Решение. В уравнении  разделяем переменные:
разделяем переменные:

 .
.
Интегрируя обе части уравнения, находим  где
где  постоянная. Таким образом,
постоянная. Таким образом,  общее решение. Интегральные кривые представляют собой параболы, которые переходят друг в друга при параллельном переносе вершины по оси абсцисс.
общее решение. Интегральные кривые представляют собой параболы, которые переходят друг в друга при параллельном переносе вершины по оси абсцисс.
Нетрудно видеть, что 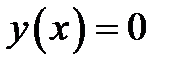 является стационарным решением уравнения. Поскольку через каждую точку оси абсцисс проходят по крайней мере пара интегральных кривых (парабола и сама ось), то
является стационарным решением уравнения. Поскольку через каждую точку оси абсцисс проходят по крайней мере пара интегральных кривых (парабола и сама ось), то 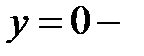 особое решение.
особое решение.
2. Решить уравнение:
а)  б)
б)  в)
в) 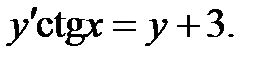
Решение. Это три уравнения с разделяющимися переменными.
а) Преобразуем уравнение и разделяем переменные:

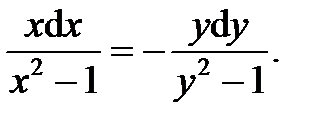
При обращении в нуль 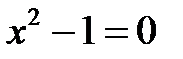 и
и  имеем четыре решения:
имеем четыре решения:  ,
,  ,
,  и
и  .
.
Интегрируя обе части уравнения  , последовательно находим
, последовательно находим


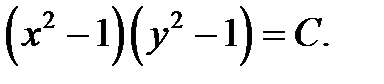
На каждом этапе преобразования постоянная интегрирования обозначается в наиболее удобном виде, при этом 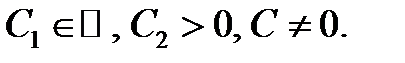 При
При 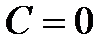 получаем все четыре выше указанных решения. Итак, общий интеграл уравнения:
получаем все четыре выше указанных решения. Итак, общий интеграл уравнения: 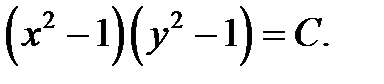
б) Заметим, что  – решение. Если
– решение. Если  , то в уравнении
, то в уравнении  разделяем переменные:
разделяем переменные:  . Интегрируя обе части уравнения, имеем
. Интегрируя обе части уравнения, имеем


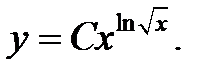
Здесь 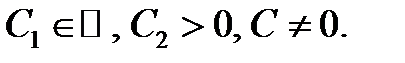 Постоянная
Постоянная  отвечает полученному ранее решению
отвечает полученному ранее решению  Итак, общеерешение уравнения
Итак, общеерешение уравнения 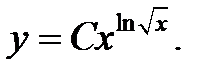
в) Непосредственной проверкой убеждаемся, что  решение уравнения. Если
решение уравнения. Если  , то разделяем переменные
, то разделяем переменные 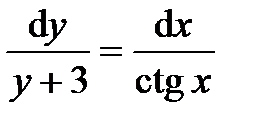 и интегрируем обе части:
и интегрируем обе части:


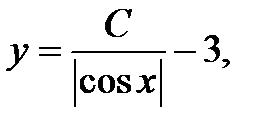
где  При
При  получаем решение
получаем решение  . Таким образом, общее решение уравнения
. Таким образом, общее решение уравнения 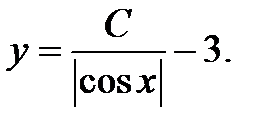
Заметим, что через точки с абсциссами  не проходит ни одной интегральной кривой уравнения за исключением точек
не проходит ни одной интегральной кривой уравнения за исключением точек  , которые принадлежат прямой
, которые принадлежат прямой  .
.

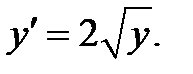
 разделяем переменные:
разделяем переменные:
 .
. где
где  постоянная. Таким образом,
постоянная. Таким образом,  общее решение. Интегральные кривые представляют собой параболы, которые переходят друг в друга при параллельном переносе вершины по оси абсцисс.
общее решение. Интегральные кривые представляют собой параболы, которые переходят друг в друга при параллельном переносе вершины по оси абсцисс.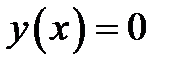 является стационарным решением уравнения. Поскольку через каждую точку оси абсцисс проходят по крайней мере пара интегральных кривых (парабола и сама ось), то
является стационарным решением уравнения. Поскольку через каждую точку оси абсцисс проходят по крайней мере пара интегральных кривых (парабола и сама ось), то 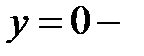 особое решение.
особое решение. б)
б)  в)
в) 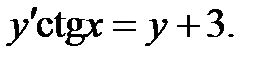

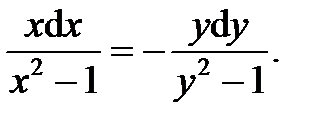
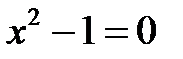 и
и  имеем четыре решения:
имеем четыре решения:  ,
,  ,
,  и
и  .
. , последовательно находим
, последовательно находим

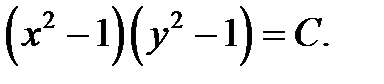
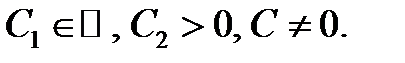 При
При 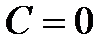 получаем все четыре выше указанных решения. Итак, общий интеграл уравнения:
получаем все четыре выше указанных решения. Итак, общий интеграл уравнения:  – решение. Если
– решение. Если  , то в уравнении
, то в уравнении  разделяем переменные:
разделяем переменные:  . Интегрируя обе части уравнения, имеем
. Интегрируя обе части уравнения, имеем

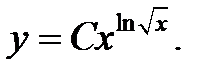
 отвечает полученному ранее решению
отвечает полученному ранее решению  Итак, общеерешение уравнения
Итак, общеерешение уравнения  решение уравнения. Если
решение уравнения. Если  , то разделяем переменные
, то разделяем переменные 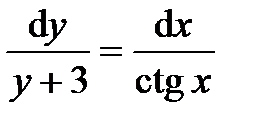 и интегрируем обе части:
и интегрируем обе части:

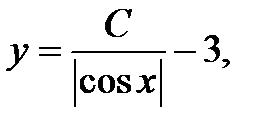
 При
При  получаем решение
получаем решение  . Таким образом, общее решение уравнения
. Таким образом, общее решение уравнения 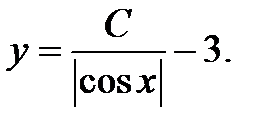
 не проходит ни одной интегральной кривой уравнения за исключением точек
не проходит ни одной интегральной кривой уравнения за исключением точек  , которые принадлежат прямой
, которые принадлежат прямой  .
.


