Алгебраические многочлены.
Многочленом степени n от переменной х называется функция вида Если a0=1, многочлен называется приведённым. Теорема о делении многочленов. Для любых двух многочленов P(x) и Q(x) можно найти такие многочлены S(x) и R(x), что P(x)=Q(x)∙S(x)+R(x), причём степень R(x) меньше степени Q(x) или же R(x) Многочлен S(x) называется частным от деления P(x) на Q(x), а R(x) – остатком от этого деления. Если остаток от деления P(x) на Q(x) равен нулю, то Q(x) называется делителем многочлена P(x). Процесс деления многочленов аналогичен процессу деления натуральных чисел “столбиком” и осуществляется таким образом, чтобы на каждом промежуточном этапе деления исчезала старшая степень делимого многочлена. Пример 1. Разделить многочлен
|
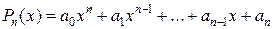, где числа a0, a1, …, an называются коэффициентами многочлена, причём a0≠0 – старший коэффициент, an – свободный член.
0. Многочлены S(x) и R(x) определяются однозначно.
на многочлен 
