Сведения о колебаниях. Гармонические колебания
Выясняя условие устойчивого равновесия системы (с. 27), нам удалось установить, если потенциальная энергия её (системы) минимальна – система находится в потенциальной яме. В этом можно убедиться, рассматривая рис. 3.1.; где по оси х отложена величина упругой деформации системы, а по оси у – значение её потенциальной энергии. Действительно, при выведении системы из положения равновесия (вправо или влево) немедленно возникает упругая сила Естественно ожидать, движение в такой системе (рис. 3.1.) совершается около положения равновесия и повторяется через какое-то время. В математике известны лишь две функции, для которых характерна периодическая повторяемость – это sin или cos. Характер движения под действием возвращающей силы поможет выяснить второй закон Ньютона
 . Здесь a является радианной мерой смещения тела из положения равновесия. Она может быть представлена через время повторяемости Т движения тела, которое принято называть периодом колебания, и через момент времени t, представляющий интерес для наблюдателя, т.е. a = w × t; где символ w = 2p/Т отражает смещение тела из положения равновесия в радианной мере, приходящееся на единицу времени; это циклическая или круговая частота. Символом А обозначено максимальное смещение из положения равновесия. . Здесь a является радианной мерой смещения тела из положения равновесия. Она может быть представлена через время повторяемости Т движения тела, которое принято называть периодом колебания, и через момент времени t, представляющий интерес для наблюдателя, т.е. a = w × t; где символ w = 2p/Т отражает смещение тела из положения равновесия в радианной мере, приходящееся на единицу времени; это циклическая или круговая частота. Символом А обозначено максимальное смещение из положения равновесия.
Скорость движения тела для написанного закона смещения от времени запишется Таким образом, движения совершаемые телом около положения равновесия, представляют собой колебательный процесс. Поскольку колебания осуществляются по закону синуса или косинуса, их принято называть гармоническими. Замечательным является то, что закон динамики накладывает условия на период возможных колебаний. Действительно, после сокращения множителей, содержащих время, из последней формулы следует В зависимости от природы взаимодействующих тел в системе различают колебания механические, электромагнитные, электромеханические; как правило, широко используемые в технике. В зависимости от характера воздействия на колебательную систему, различают свободные колебания, вынужденные колебания, автоколебания и параметрические колебания. Свободные колебания, как правило, затухающие, широко распространены в окружающей действительности; например, колебания ветки после взлёта с неё птички. Вынужденные колебания возникают в системе, подвергающейся воздействию внешней периодически изменяющейся силы, например, колебания канатного моста, когда по нему шагают, переходя на другой берег через речку. Автоколебания сопровождаются воздействием на колебательную систему внешних сил, однако моменты времени воздействия на систему извне определяется самой системой. Типичным примером являются, естественно, часы. При параметрических колебаниях за счёт внешнего воздействия происходит периодическое изменение какого-либо параметра системы; например, сохнущее бельё на верёвке и порывы ветра; что делают порывы? Рассуждайте; это полезно.
|

 , стремящаяся вернуть систему в устойчивое состояние х = 0, соответствующее минимуму потенциальной энергии. Ранее было установлено (с. 23), потенциальная энергия при малых деформациях выражается формулой
, стремящаяся вернуть систему в устойчивое состояние х = 0, соответствующее минимуму потенциальной энергии. Ранее было установлено (с. 23), потенциальная энергия при малых деформациях выражается формулой  ; взяв производную, формула силы упругости примет вид:
; взяв производную, формула силы упругости примет вид:  . Смысл знака минус в том, что найденная сила всегда возвращает тело к положению равновесия, всегда направлена в сторону противоположную смещению.
. Смысл знака минус в том, что найденная сила всегда возвращает тело к положению равновесия, всегда направлена в сторону противоположную смещению. ; здесь сила
; здесь сила  и закон динамики принимает вид
и закон динамики принимает вид  .
.
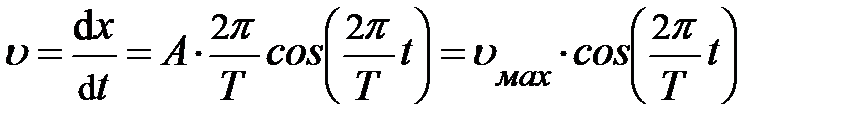 ; где
; где 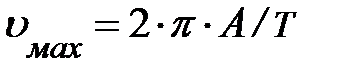 . Ускорение найдём как производную скорости
. Ускорение найдём как производную скорости  , где
, где  . Подставим выражения для ускорения и для смещения в закон динамики
. Подставим выражения для ускорения и для смещения в закон динамики  ; множители, содержащие время, сокращаются. Следовательно, предложенное уравнение движения для малых отклонений от равновесия (вблизи дна потенциальной ямы)
; множители, содержащие время, сокращаются. Следовательно, предложенное уравнение движения для малых отклонений от равновесия (вблизи дна потенциальной ямы)  удовлетворяет второму закону динамики.
удовлетворяет второму закону динамики. , или
, или  . Отсюда следует, простейшая колебательная система должна содержать два тела. В рассмотренном примере тело массы m проявляет инертные свойства к изменению своего положения, а упругое тело с коэффициентом жёсткости k «препятствует» появлению деформации. Эти противоречивые свойства тел, разумно объединённые в системе, порождают новое качество – повторяемость событий в системе и через свои характеристики определяют период её собственных колебаний.
. Отсюда следует, простейшая колебательная система должна содержать два тела. В рассмотренном примере тело массы m проявляет инертные свойства к изменению своего положения, а упругое тело с коэффициентом жёсткости k «препятствует» появлению деформации. Эти противоречивые свойства тел, разумно объединённые в системе, порождают новое качество – повторяемость событий в системе и через свои характеристики определяют период её собственных колебаний.


