Вращательное движение
Вращательное движение является частным случаем криволинейного движения. Кроме того, будем рассматривать движение материальной точки по окружности с постоянной по модулю скоростью, Пусть точечное тело (материальная точка) движется по окружности радиуса R (рис. 1.3). За некоторый промежуток времени Dt оно пройдёт путь DS, равный дуге АВ. В точке А тело имело скорость
 . Геометрическая иллюстрация вращательного движения (рис. 3) позволяет эту запись представить следующим образом: . Геометрическая иллюстрация вращательного движения (рис. 3) позволяет эту запись представить следующим образом:  . Прочитать её можно так: вектор . Прочитать её можно так: вектор  , характеризующий изменение скорости по направлению, представляет собой сумму векторов ( , характеризующий изменение скорости по направлению, представляет собой сумму векторов (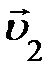 ) и (– ) и (–  ) и соединяет начало первого вектора ( ) и соединяет начало первого вектора (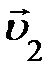 ) с концом второго вектора (– ) с концом второго вектора (–  ), рис. 1.3. Это позволяет выразить модуль, численное значение вектора ), рис. 1.3. Это позволяет выразить модуль, численное значение вектора  через кинематические характеристики: скорость и радиус окружности. Действительно, ÐАОВ = ÐВСD как углы с взаимно перпендикулярными сторонами (построением убедились?; можно рассуждениями); по числовому значению скорость постоянна и через кинематические характеристики: скорость и радиус окружности. Действительно, ÐАОВ = ÐВСD как углы с взаимно перпендикулярными сторонами (построением убедились?; можно рассуждениями); по числовому значению скорость постоянна и  . Следовательно, rАОВ и rВСD подобны по двум сторонам и углу между ними (почему?), отсюда из rВСD следует . Следовательно, rАОВ и rВСD подобны по двум сторонам и углу между ними (почему?), отсюда из rВСD следует  , а из rАОВ этот же угол , а из rАОВ этот же угол  (см. рис. 1.3.). Поскольку левые части уравнений равны (углы с взаимно перпендикулярными сторонами), то из правых частей немедленно следует, модуль, численное значение вектора (см. рис. 1.3.). Поскольку левые части уравнений равны (углы с взаимно перпендикулярными сторонами), то из правых частей немедленно следует, модуль, численное значение вектора 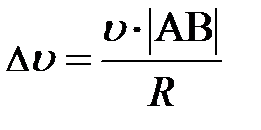 (самостоятельно проделали?). По определению ускорение, в нашем случае характеризующее изменение скорости по направлению, равно (самостоятельно проделали?). По определению ускорение, в нашем случае характеризующее изменение скорости по направлению, равно  . Если промежуток времени Dt взять малым, то хорда АВ стремится к длине дуги АВ, или пройденному пути DS за время Dt. Перепишите на листке аналитическое выражение ускорения (а) и самостоятельно замените в нём . Если промежуток времени Dt взять малым, то хорда АВ стремится к длине дуги АВ, или пройденному пути DS за время Dt. Перепишите на листке аналитическое выражение ускорения (а) и самостоятельно замените в нём 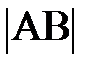 на пройденный путь DS. Поскольку DS/Dt = на пройденный путь DS. Поскольку DS/Dt =  , для символической записи ускорения, характеризующего быстроту изменения скорости по направлению, получим выражение , для символической записи ускорения, характеризующего быстроту изменения скорости по направлению, получим выражение 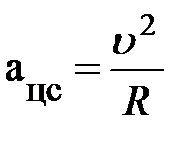 (преобразования проделайте самостоятельно). Направление центростремительного ускорения можно определить по рис. 1.3. Из треугольника скоростей, rВСD следует, чем меньше промежуток времени Dt, тем меньше угол D j. При этом векторы (преобразования проделайте самостоятельно). Направление центростремительного ускорения можно определить по рис. 1.3. Из треугольника скоростей, rВСD следует, чем меньше промежуток времени Dt, тем меньше угол D j. При этом векторы  и и  , имеют одинаковое направление и направлены по радиусу R окружности к её центру O. , имеют одинаковое направление и направлены по радиусу R окружности к её центру O.
При рассмотрении равномерного движения по окружности привлекались как линейные кинематические характеристики перемещение, путь, скорость, ускорение, радиус окружности, так и угловая характеристика – угол поворота Dj, опирающийся на отрезок АВ. Появление угла поворота связано с линейными величинами, естественно желание прописать равномерное движение материальной точки по окружности и через угловые характеристики. При вращательном движении угол поворота является основной кинематической характеристикой и с точки зрения количественной математики в общем виде может быть записан следующим образом: Dj = = j2 –.j1 = j2 = j = 2×p×N; если j1 = 0. Прочитаем эту запись: изменение угла поворота Dj равно разности конечного (j2) и начального (j1) значений; если же начальный угол j1 = 0, обозначать конечное значение значком j2 не имеет смысла и цифру два опускают. Итак, угол поворота j = 2×p×N, естественно, это произошло за время Dt; здесь 2p = 360о и представляет собой один полный оборот, N – число оборотов за время движения; не обязательно полных, например, 0,37. Отношение угла поворота к времени, в течение которого это изменение произошло, будет характеризовать изменение угла поворота в единицу времени, то есть это быстрота изменения угла поворота или угловая скорость w. Аналитически это может быть представлено следующим образом: Ещё две характеристики, полезные для технических целей, могут быть введены из уравнения: j = 2p×N = w×t. Действительно, если N = 1, уравнение примет вид: 2p×1 = w×t. Здесь t время одного полного оборота. Его принято обозначать буквой Т – время одного оборота. Тогда 2p = w×Т, отсюда следует Для снятия сомнений в понятии «малые углы», проделайте следующие действия: воспользуйтесь тригонометрической таблицей или калькулятором и найдите sin10о. Нашли? Запишите это значение. Проделайте следующие действия: 2p радиан равны 360о; найдите операцией «деление» сколько в одном градусе радиан; нужно 2p разделить на 360о, разделили?; не забыли, что p = 3,14 радиан?; умножьте на 10о. Если уже умножили, сопоставьте с табличным результатом или найденным по калькулятору. В каком знаке ошибка? Вы с такой точностью умеете считать? Можно ли согласиться с понятием «малые углы»? Наверное, всё-таки можно! В заключение две дежурные задачи. Запишите центростремительное ускорение через угловую скорость; период обращения, частоту вращения. Введение угловых характеристик позволяет записать уравнение движения тела по окружности через угловые характеристики. Как будет выглядеть уравнение движения: j = f(t) через угловую скорость; период вращения; частоту вращения?; это и есть вторая задача. Завершая экскурс в раздел кинематики «вращательное движение», перечислим его ключевые слова: угол поворота, малый промежуток времени, угловая скорость, центростремительное ускорение, период вращения, частота вращения.
|

 . Это упрощает строгость аналитического рассмотрения и позволяет удовлетвориться геометрической иллюстрацией.
. Это упрощает строгость аналитического рассмотрения и позволяет удовлетвориться геометрической иллюстрацией.
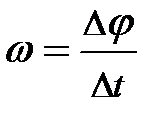 . Поскольку появление угловых характеристик обусловлено наличием линейных, естественно ожидать взаимосвязь между угловой и линейной скоростями. Ранее нам удалось показать, что
. Поскольку появление угловых характеристик обусловлено наличием линейных, естественно ожидать взаимосвязь между угловой и линейной скоростями. Ранее нам удалось показать, что  и тогда немедленно следует:
и тогда немедленно следует: 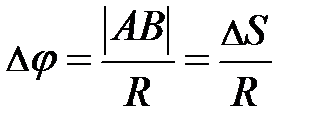 . Подставляя в аналитическое выражение угловой скорости, получим
. Подставляя в аналитическое выражение угловой скорости, получим  , то есть угловая скорость связана с линейной скоростью выражением
, то есть угловая скорость связана с линейной скоростью выражением  (преобразования проделали самостоятельно?).
(преобразования проделали самостоятельно?). , а
, а  . Если известно время одного полного оборота, а единицу времени одну секунду разделить на время одного оборота, получим вторую характеристику движения материальной точки по окружности; или для вращательного движения. Её принято называть частотой вращения
. Если известно время одного полного оборота, а единицу времени одну секунду разделить на время одного оборота, получим вторую характеристику движения материальной точки по окружности; или для вращательного движения. Её принято называть частотой вращения  . Единицей измерения периода является секунда (с); единицей частоты вращения герц (Гц). 1 Гц – частота периодического процесса, при которой за время, равное одной секунде, происходит один цикл периодического процесса.
. Единицей измерения периода является секунда (с); единицей частоты вращения герц (Гц). 1 Гц – частота периодического процесса, при которой за время, равное одной секунде, происходит один цикл периодического процесса.


