Энергия
Основная задача механики – нахождение движения тела по заданным силам. Найти движение – это значит суметь указать, в каком месте пространства, и в какой момент времени находится движущееся тело. Чтобы справиться с такой задачей, нужно располагать исчерпывающими сведениями о действующих силах. Силы должны быть известны для любой точки и любого места нахождения этого тела. Если силы известны, уравнения Ньютона позволяют определить ускорение движущегося тела. Однако при помощи одних только уравнений движения Ньютона сведения о траектории, скорости, знании момента времени, которому соответствует прохождение через данную точку пространства, не могут быть получены. Чтобы прописать движение, надо знать для любого момента времени место, где находилось тело, а также его скорость как по величине, так и по направлению. Эти данные (х, Итак, механическое состояние тела само по себе измениться не может, необходимо действие со стороны других тел; наличие силы. Будем рассуждать так. Пусть под действием силы происходит изменение механического состояния тела. Тогда должна быть физическая величина, являющаяся мерой изменения этого состояния, которая зависит как от величины силы Работа является скалярной величиной; имеет только численное значение. Вместе с тем это величина алгебраическая: если cosa>0, работа положительна; если cosa<0, работа отрицательна. При a = p/2 работа равна нулю. Это обстоятельство особенно отчётливо показывает, что понятие работы в механике существенно отличается от обыденного представления о работе. Найдём работу, совершаемую при растяжении или сжатии пружины, рис. 2.6.. Чтобы выполнялся закон Гука
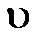 ); движение равноускоренное, рис. 2.7., сила ); движение равноускоренное, рис. 2.7., сила 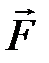 > > 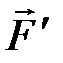 . По второму закону динамики равнодействующая сил . По второму закону динамики равнодействующая сил 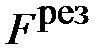 = = 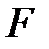 – – 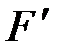 = m × a и под действием её совершается работа А = = m × a и под действием её совершается работа А = 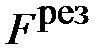 ×DS= = m × a ×DS, где а – среднее ускорение на участке пути DS, равное а = D ×DS= = m × a ×DS, где а – среднее ускорение на участке пути DS, равное а = D 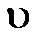 /D t. Подставляя ускорение в формулу работы, получаем уравнение вида: А = = m ×D /D t. Подставляя ускорение в формулу работы, получаем уравнение вида: А = = m ×D 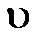 ×DS/D t, где DS/D t = ×DS/D t, где DS/D t = 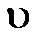 – средняя скорость на участке пути DS и тогда аналитическое выражение работы принимает вид: А = m ×D – средняя скорость на участке пути DS и тогда аналитическое выражение работы принимает вид: А = m ×D 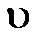 × × 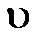 . Учитывая, что . Учитывая, что  и и 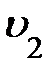 мгновенные скорости в начале и в конце пути DS, изменение скорости D мгновенные скорости в начале и в конце пути DS, изменение скорости D 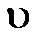 = = 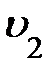 – –  , а средняя скорость на этом участке , а средняя скорость на этом участке 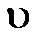 = ( = (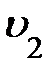 + +  )/2, и тогда конечное выражение для работы принимает вид: А = )/2, и тогда конечное выражение для работы принимает вид: А = 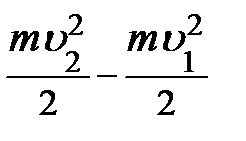 . .
Въедливому читателю преобразования проделать самостоятельно. Итак, приведённые примеры показали, когда есть взаимодействие тел, сопровождающееся изменением механического состояния, совершается работа. Совершённая работа равна разности некоей физической величины, содержащей параметры начального и конечного механических состояний. Физическая величина обязательно является функцией состояния – положения тел х и скорости движения На практике большое значение имеет не только величина совершённой работы, но и время, в течение которого она совершается. Поэтому для характеристики механизмов, предназначенных для совершения работы, вводится понятие мощности. Новая величина, равная отношению работы к промежутку времени, за которое эта работа совершается Завершая экскурс в раздел динамики «Понятие механического состояния. Работа. Мощность. Энергия», перечислим его ключевые слова: механическое состояние, механическая работа, мощность, энергия потенциальная и кинетическая, закон сохранения энергии.
|

 ; растяжение, сжатие будем производить медленно. В выражение работы следует подставить среднее значение силы
; растяжение, сжатие будем производить медленно. В выражение работы следует подставить среднее значение силы  , то есть
, то есть  (почему?). После преобразований аналитическое выражение работы по растяжению, сжатию пружины как по величине, так и по знаку одинаково и примет вид:
(почему?). После преобразований аналитическое выражение работы по растяжению, сжатию пружины как по величине, так и по знаку одинаково и примет вид:  ; желательно проделать преобразования самостоятельно. Здесь учтено, в момент начала сжатия х 1 =
; желательно проделать преобразования самостоятельно. Здесь учтено, в момент начала сжатия х 1 = 

 , показывает, какую работу данное устройство может совершить за единицу времени. Поскольку DА = F×DS, а DS/D t равно средней скорости на пути DS, то среднее значение мощности за время D t равно N = F×
, показывает, какую работу данное устройство может совершить за единицу времени. Поскольку DА = F×DS, а DS/D t равно средней скорости на пути DS, то среднее значение мощности за время D t равно N = F× 


