Оценка эффективности использования ресурсного потенциала на основе корреляционно-регрессионного анализа
Производственный потенциал представляет собой обобщающий показатель ресурсообеспеченности сельского хозяйства, и его расчет состоит в определении суммарной оценки всех ресурсов. Основная трудность в построении такого показателя заключается в несоизмеримости различных видов ресурсов: земельных, трудовых и материальных. Теоретической основой их соизмерения является концепция взаимозаменяемости разных видов ресурсов в процессе производства. Элементы ресурсного потенциала, с одной стороны, качественно однородны по функциональному признаку, так как все они представляют собой ресурсы, предопределяющие результаты производственной деятельности. С другой стороны, ресурсный потенциал является синтетическим расчетным показателем, который нельзя непосредственно измерить. Поэтому разработка соответствующего инструментария всегда имела большое теоретическое и практическое значение, а сейчас, в условиях развития рыночных отношений, когда возрастает роль экономических методов государственного регулирования, эта проблема становится еще более актуальной. В российской аграрной экономике предлагаются различные методы количественной оценки использования ресурсного потенциала предприятия. Наиболее приемлем для расчета комплексного показателя оценки ресурсного потенциала подход, основанный на корреляционно-регрессионном анализе, который нашел свое отражение в работах экономистов Смагина Б.И, Акиндинова В.В., Т. Шаталовой и др. С теоретической точки зрения, в качестве обобщающего результативного показателя комплексной оценки необходимо использовать выход товарной продукции сельского хозяйства на 1 га сельскохозяйственных угодий. На наш взгляд, в рыночных условиях целесообразнее в качестве результата рассматривать показатель товарной продукции сельского хозяйства на единицу площади. Аргументом в пользу выбора данного показателя является и тот факт, что в сельском хозяйстве значительная часть произведенной продукции не реализуется, а используется повторно в процессе производства. Поскольку цель любого производства – получение прибыли, то стоимость товарной продукции является важнейшей составляющей ее формирования. Однако однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков позволяет корреляционно-регрессионный метод анализа, который дает возможность исследовать зависимость выхода товарной продукции в расчете на 1 га сельскохозяйственных угодий (у) от следующих факторов: х1- трудообеспеченность, чел.; х2- фондообеспеченность, руб.; х3– энергообеспеченность, л.с. х4- производственные затраты на 100 га сельскохозяйственных угодий, руб. Таблица 27 – Исходные данные для корреляционно-регрессионного анализа производственного потенциала
Динамика необходимых показателей для корреляционно-регрессионного анализа производственного потенциала представлена в таблице 28.
Таблица 28 - Результативные и факторные показатели производственного потенциала
Показатель вариации Vy= где σ - стандартное отклонение; у, х - среднее значение; Vy =
Так как переменные х1, х2, х3, х4 слабо варьируют от средней величины, то можно сделать ввод о низком уровне варьирования. Показатель вариации по результативному показателю (у) составил 13,5. Для изучения связи между показателями будем использовать метод наименьших квадратов и вероятностные методы оценки статистических гипотез. Значение коэффициента в парной корреляции указывает на весьма тесную связь выхода товарной продукции в расчете на 1 га (у) с затратами на производство продукции на 100 га (х4).
но в то же время весьма тесная межфакторная связь между х2 и х4
Далее необходимо составить уравнение вида: у = b0 + b1x1 + b2x2 +b3x3 + b4x4. b – коэффициенты при переменных величинах. Для определения коэффициентов воспользуемся таблицей «регрессия»: у = 14768,41+ 0,13x1 -3,76x2 -3639,07x3 +0,02x4 Значение стандартных ошибок, параметров b0, b1, b2, b3, b4 с учетом округления: mb0 = 3094,41; mb1 = 0,13; mb2 = 0,82; mb3 = 1391,89; mb4 = 0,01; Они показывают, какое значение данной характеристики сформировалось под влиянием случайных факторов. Эти значения используются для расчета t-критерия Стьюдента (t - статистика). tb0 = 4,77; tb1 = 65535; tb2 = -4,57; tb3 = -2,61; tb4 = 6,79; Если значения t - критерия больше 2-3 (чаще всего 2,5) можно сделать вывод о существенности данного параметра, который формируется под воздействием неслучайных величин. Здесь статистически значимыми являются все показатели. На это же указывает показатель вероятности случайных значений параметров регрессии. Если α (Р – значение) больше чем 10% (0,1), то фактор можно считать случайным и неинформативным и удалить его для дальнейшего улучшения уравнения. В нашем случае α равняется 13,14%, 13,71% и 23,25% что больше 10%, поэтому факторы х1 и х2 можно отбросить из нашего уравнения, для его улучшения. Величина b1 = 0,13 оценивает агрегированное влияние прочих факторов на результативный показатель. По данным таблицы дисперсионного анализа F фактическое = 957,72. Вероятность случайно получить такое значение F критерия составляет 0,00000003, что не превышает допустимый уровень значимости 5%, следовательно, полученное значение не случайно. Об этом свидетельствует величина Р-значения из этих же таблиц. Полученное значение сформировалось под влиянием существенных факторов, то есть подтверждается статистическая значимость всего уравнения и показателя тесноты связи Скорректированный коэффициент множественной детерминации Оба коэффициента указывают на высокую детерминированность результата у в модели с факторами х1, х2, х3, х4.
|

 * 100;
* 100;  =
=  * 100;
* 100;  =
=  * 100;
* 100;  =
=  * 100;
* 100; * 100 = 13,5;
* 100 = 13,5; =
=  * 100 = 0;
* 100 = 0; * 100 = 6,74;
* 100 = 6,74; * 100 = 11,27;
* 100 = 11,27; * 100 = 20,24;
* 100 = 20,24;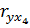 = 0,965
= 0,965 = 0,914
= 0,914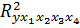 нескорректированный коэффициент множественной детерминации
нескорректированный коэффициент множественной детерминации 


