Множества на прямой
Пусть а < b. Напомним, что отрезок [ a, b ] определяется неравенствами а £ x £ b; интервал (a, b) – неравенствами а < x < b (при этом допускается, что а = – ¥ или (и) b = + ¥); полуинтервал [ a, b) – неравенствами а £ x < b; и, наконец, полуинтервал (a, b ] – неравенствами а < x £ b. Далее, определим окрестность точки. С этой целью напомним, что
Эквивалентное определение модуля таково:
Например, Модуль есть расстояние от точки до нуля.
Множество точек x, удовлетворяющих этому неравенству (т.е. отстоящих от а менее чем на e), назовем e- окрестностью точки а, или просто окрестностью точки а. Обозначим ее
Пересечение конечного числа открытых есть открытое множество (Пустое множество открыто по определению). Множество В = ú\ А называется дополнением к А (в ú) и обозначается CA. Оно состоит из всех точек x Ï А. Множество F называется замкнутым, если дополнение к нему открыто. Например, отрезок [ a, b ] есть замкнутое множество, поскольку дополнение к нему есть (– ¥, а) È (b, + ¥) – открытое множество.
Множества Æ и ú открыты и замкнуты одновременно. Полуинтервал [ a, b) (а < b) – пример множества ни открытого, ни замкнутого. Пересечение любого числа замкнутых множеств есть замкнутое множество. Объединение конечного числа замкнутых есть замкнутое множество. Множество А называется ограниченным, если $ М > 0 такое, что
|


 .
. ;
;  .
.
 Следовательно,
Следовательно,  есть расстояние между x и y:
есть расстояние между x и y:








 Пусть e > 0 – число. Неравенство
Пусть e > 0 – число. Неравенство 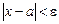 равносильно двойному неравенству a – e < x < a + e:
равносильно двойному неравенству a – e < x < a + e: . Окрестность
. Окрестность 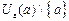 , будем называть проколотой окрестностью точки а.
, будем называть проколотой окрестностью точки а.
 Множество G называется открытым, если вместе с каждой своей точкой оно содержит и некоторую ее окрестность. Например, интервал (a, b) есть открытое множество.
Множество G называется открытым, если вместе с каждой своей точкой оно содержит и некоторую ее окрестность. Например, интервал (a, b) есть открытое множество.
 Объединение любого числа открытых множеств есть открытое множество.
Объединение любого числа открытых множеств есть открытое множество.

 " x Î A, т.е. А Ì [– М, М ]. Ограниченное и замкнутое множество на прямой называют также компактным множеством, или компактом. Например, отрезок [ a, b ] – компакт.
" x Î A, т.е. А Ì [– М, М ]. Ограниченное и замкнутое множество на прямой называют также компактным множеством, или компактом. Например, отрезок [ a, b ] – компакт.


