Сложная функция, или суперпозиция
Тогда можно построить отображение из Х в Z по правилу z = g (f (x)) " х Î Х, т.е. элементу х отображение f сопоставляет элемент у = f (х), а элементу у отображение g сопоставляет элемент z = g (y) = g (f (x)). Тем самым определена функция F: X ® Z такая, что F (x) = g (f (x)) " х Î Х. Она обозначается Например, если y = x 2 = f (x), а z = sin y = g (y), то F (x) = g (f (x)) = sin x 2 – сложная функция, полученная как суперпозиция «квадрата» и синуса.
Обратная функция Пусть x = g (y) Û y = f (x) и, следовательно g (f (x)) = x " х Î Х; f (g (y)) = y " у Î Y.
Пример Всюду в дальнейшем область определения и область значений функции – подмножества числовой оси.
В этом и состоит «правило», по которому каждому аргументу х ставится в соответствие значение функции у = sin х. При этом областью определения служит вся числовая ось ú. Область значений можно выбирать по-разному. Если взять Y = ú, то отображение не будет сюръективным. Поэтому положим Y = [–1, 1], и тогда sin: ú
(f (– x) = – f (x)) и принимает все свои зна  чения от – 1 до 1. Итак, чения от – 1 до 1. Итак,
Следовательно, существует обратная функция
Она также является нечетной. Если arcsin y = x Û y = sin x и, следовательно, arcsin (sin x) = х
ЗАДАНИЕ. Вспомните определения arccos x и arctg x.
|









 Пусть даны три множества X, Y, Z и два отображения f: X ® Y и g: Y ® Z.
Пусть даны три множества X, Y, Z и два отображения f: X ® Y и g: Y ® Z. и называется сложной функцией или суперпозицией отображений f и g.
и называется сложной функцией или суперпозицией отображений f и g. – биекция. Построим отображение из Y в Х следующим образом. Возьмем произвольный элемент у Î Y. Поскольку f отображает «на», то у него обязательно имеется прообраз х, т.е. такой элемент, что f (x) = y. Этот прообраз является единственным, поскольку отображение f взаимно-однозначно. Итак, произвольному у Î Y мы сопоставили единственный х Î Х. Обозначим его х = g (y). Мы получили отображение g: Y ® X, которое называется обратным к отображению f: X ® Y и обозначается g = f – 1. При этом для х Î Х и у Î Y имеем
– биекция. Построим отображение из Y в Х следующим образом. Возьмем произвольный элемент у Î Y. Поскольку f отображает «на», то у него обязательно имеется прообраз х, т.е. такой элемент, что f (x) = y. Этот прообраз является единственным, поскольку отображение f взаимно-однозначно. Итак, произвольному у Î Y мы сопоставили единственный х Î Х. Обозначим его х = g (y). Мы получили отображение g: Y ® X, которое называется обратным к отображению f: X ® Y и обозначается g = f – 1. При этом для х Î Х и у Î Y имеем






 Напомним определение функции у = sin х: дуге х единичной окружности сопоставляется проекция на вертикальную ось соответствующего радиус-вектора, составляющего с горизонтальной осью угол х (см. рис.).
Напомним определение функции у = sin х: дуге х единичной окружности сопоставляется проекция на вертикальную ось соответствующего радиус-вектора, составляющего с горизонтальной осью угол х (см. рис.).


 [–1, 1] – сюръекция. Но поскольку sin периодическая функция, инъекцией это отображение не является. Чтобы получить 1:1 функцию, надо сузить область определения до какого-либо отрезка монотонности синуса. Выберем от
[–1, 1] – сюръекция. Но поскольку sin периодическая функция, инъекцией это отображение не является. Чтобы получить 1:1 функцию, надо сузить область определения до какого-либо отрезка монотонности синуса. Выберем от 




 резок
резок  . Он хорош тем, что
. Он хорош тем, что 
 симметричен относительно нуля, на
симметричен относительно нуля, на 
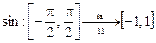 – биекция.
– биекция. .
. ,
,  , то
, то ; sin (arcsin y) = y
; sin (arcsin y) = y  .
.


