Полные квадратные уравнения:
 - общего вида и приведённое:
- общего вида и приведённое: 
Корни ищутся по формуле:  ,где
,где 
Сокращённые квадратные уравнения:
 , тогда:
, тогда:  , тогда:
, тогда:
 надо выразить x2 вынести x за скобку
надо выразить x2 вынести x за скобку 

Биквадратные уравнения имеют вид: 
Решаются в два этапа.
1-ый этап: путем замены  ,исходное уравнение приводится к квадратному:
,исходное уравнение приводится к квадратному:  и решается обычным образом. Если найдены корни
и решается обычным образом. Если найдены корни  переходим ко второму этапу, если квадратное уравнение не имеет корней, то и соответствующее биквадратное так же не имеет корней.
переходим ко второму этапу, если квадратное уравнение не имеет корней, то и соответствующее биквадратное так же не имеет корней.
2-ой этап: решаем уравнение замены  для каждого корня
для каждого корня  .
.


Примечание. Если значение  , то соответствующее уравнение
, то соответствующее уравнение  не имеет корней.
не имеет корней.
Пример.  пусть
пусть  , тогда
, тогда

Вернёмся к уравнению замены:
1)  2)
2) 
Ответ:  .
.
Дробно рациональные уравнения.
 , где
, где  называются рациональными. Решение такого уравнения сводится к решению уравнения
называются рациональными. Решение такого уравнения сводится к решению уравнения  и проверки условия ОДЗ:
и проверки условия ОДЗ: 
Прим.

Замечание: решение уравнения надо начинать с приведения к общему виду.
Системы уравнений решаются двумя способами:
Способ сложения
Прим.  домножаем обе части второго уравнения на -2;
домножаем обе части второго уравнения на -2;
 ; складываем соответствующие части двух уравнений (первое без изменений)
; складываем соответствующие части двух уравнений (первое без изменений)
 ; теперь второе уравнение содержит одну неизвестную, находим её
; теперь второе уравнение содержит одну неизвестную, находим её
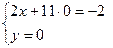 ; подставляем значение найденной неизвестной в первое уравнение
; подставляем значение найденной неизвестной в первое уравнение
 Ответ: (-1;0) либо:
Ответ: (-1;0) либо:  , либо:
, либо:  ,
,  .
.

 - общего вида и приведённое:
- общего вида и приведённое: 
 ,где
,где 
 , тогда:
, тогда:  , тогда:
, тогда: надо выразить x2 вынести x за скобку
надо выразить x2 вынести x за скобку 


 ,исходное уравнение приводится к квадратному:
,исходное уравнение приводится к квадратному:  и решается обычным образом. Если найдены корни
и решается обычным образом. Если найдены корни  переходим ко второму этапу, если квадратное уравнение не имеет корней, то и соответствующее биквадратное так же не имеет корней.
переходим ко второму этапу, если квадратное уравнение не имеет корней, то и соответствующее биквадратное так же не имеет корней.

 , то соответствующее уравнение
, то соответствующее уравнение  пусть
пусть  , тогда
, тогда
 2)
2) 
 .
. , где
, где  называются рациональными. Решение такого уравнения сводится к решению уравнения
называются рациональными. Решение такого уравнения сводится к решению уравнения  и проверки условия ОДЗ:
и проверки условия ОДЗ: 

 домножаем обе части второго уравнения на -2;
домножаем обе части второго уравнения на -2; ; складываем соответствующие части двух уравнений (первое без изменений)
; складываем соответствующие части двух уравнений (первое без изменений) ; теперь второе уравнение содержит одну неизвестную, находим её
; теперь второе уравнение содержит одну неизвестную, находим её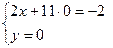 ; подставляем значение найденной неизвестной в первое уравнение
; подставляем значение найденной неизвестной в первое уравнение Ответ: (-1;0) либо:
Ответ: (-1;0) либо:  ,
,  .
.


