Графическое решение.
Пусть прямые заданы уравнениями: Признак параллельности прямых: Признак перпендикулярности прямых: Пример1. а) б) Пример2. определить проходит ли прямая Решение: если прямая проходит через точку А, то ее координаты должны удовлетворять уравнению прямой. Подставим координаты в уравнение: Пример3. Составить уравнение прямой, проходящей через точки А(1;2) и В(3;6). Решение: координаты данных точек должны удовлетворять уравнению прямой. Для определения неизвестных параметров составим систему уравнений:
Графическое решение уравнений, систем уравнений и неравенств. 1.Пусть имеется уравнение 2.Пусть имеется уравнение 3.Пусть имеется система уравнений
Рис.1 Рис.2 Рис.3. 4.Пусть имеется неравенство 5.Пусть имеется неравенство
Рис.4. Рис.5. Арифметическая прогрессия. Опр. Числовой последовательностью называется упорядоченный набор элементов (элементами являются числа), для которого известен закон получения элемента с любым номером. Пример1: 1; -4;0; 0; -1;0,2; 5; 1000, 2… - не является числовой последовательностью. Пример2: 2; 4; 6; 8;… - является числовой последовательностью. Пример3: -1;0;1;-1;0;1;-1… - является числовой последовательностью. Последовательность может быть задана несколькими способами: 1. формулой n -ного члена:
2. частью последовательности (как в примерах 2 и 3) по которой можно понять закономерность. Иногда это бывает не так просто: -1;6;-5;20…- кажется, что закономерности нет, но формула 3. Формулой выражающей следующий член через предыдущий:
Найдем несколько членов последовательности:
Опр. арифметической прогрессией называется последовательность, в которой каждый член, начиная со второго, равен предыдущему, сложенному с одним и тем же числом. Это число называется разностью арифметической прогрессии. Формула н-ного члена арифм. прогр.: Формула суммы n-первых членов арифм. прогр.: Пример.
Сумму первых 10 членов найдем по второй формуле т.к. неизвестен
Спец формула: Геометрическая прогрессия. Опр. геометрической прогрессией называется последовательность в которой каждый член начиная со второго равен предыдущему, умноженному на одно и то же число. Это число называется знаменателем геометрической прогрессии. Формула н-ного члена геом. прогр.: Формула суммы n-первых членов геом. прогр.: Формула суммы членов бесконечно убывающей геометрической прогрессии: Пример.
Сумму первых 10 членов найдем по второй формуле т.к. неизвестен
Спец формула:
|

 и
и 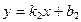


 и
и  параллельны;
параллельны; и
и  перпендикулярны;
перпендикулярны; не проходит.
не проходит. ; решая систему, получим k=2, b=0. Т.о. уравнение искомой прямой:
; решая систему, получим k=2, b=0. Т.о. уравнение искомой прямой: 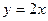
 . Тогда решением данного уравнения являются абсциссы (координаты по Ох) точек пересечения графиков функций
. Тогда решением данного уравнения являются абсциссы (координаты по Ох) точек пересечения графиков функций 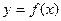 и
и 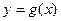 . Рис1.
. Рис1.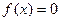 . Тогда решением данного уравнения являются абсциссы (координаты по Ох) точек пересечения графика функции
. Тогда решением данного уравнения являются абсциссы (координаты по Ох) точек пересечения графика функции  . Тогда решением данной системы являются координаты (х;у) точек пересечения графиков
. Тогда решением данной системы являются координаты (х;у) точек пересечения графиков 


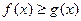 . Тогда решением будет интервал (по Ох) на котором график функции
. Тогда решением будет интервал (по Ох) на котором график функции  . Тогда решением будет интервал (по Ох) на котором график функции
. Тогда решением будет интервал (по Ох) на котором график функции 

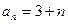 . Найдем несколько членов этой последовательности:
. Найдем несколько членов этой последовательности:  ,
,  ,
, 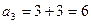 . При этом способе задания последовательности можно сразу вычислить член с любым номером, например:
. При этом способе задания последовательности можно сразу вычислить член с любым номером, например:  .
. подходит. Для такой последовательности перечисление первых членов является неудачным способом задания.
подходит. Для такой последовательности перечисление первых членов является неудачным способом задания.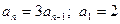 . Здесь должно быть задано значение первого члена. Для того чтобы найти значение какого-либо члена последовательности, необходимо найти все предыдущие.
. Здесь должно быть задано значение первого члена. Для того чтобы найти значение какого-либо члена последовательности, необходимо найти все предыдущие. ,
,  ,
,  .
. - n -ный член,
- n -ный член, 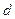 - разность арифм. прогр..
- разность арифм. прогр..
 ;
; ,
,  . Составить формулу н-ного члена арифм. прогр.. Найти первые 5 членов,
. Составить формулу н-ного члена арифм. прогр.. Найти первые 5 членов,  , сумму 10 первых членов.
, сумму 10 первых членов. ;
; 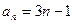
 - нашли по формуле,
- нашли по формуле, 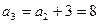 - нашли по опр. арифм. прогр.,
- нашли по опр. арифм. прогр., 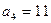 ,
, 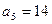 .
. .
.
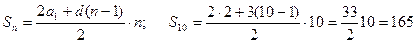 .
. .
. - n -ный член,
- n -ный член,  - знаменатель геометр. прогр..
- знаменатель геометр. прогр..
 ;
;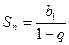 .
.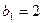 ,
,  . Составить формулу н-ного члена арифм. прогр.. Найти первые 4 члена,
. Составить формулу н-ного члена арифм. прогр.. Найти первые 4 члена,  , сумму 10 первых членов.
, сумму 10 первых членов. ;
; 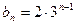
 - нашли по формуле,
- нашли по формуле,  - нашли по опр. арифм. прогр.,
- нашли по опр. арифм. прогр.,  .
. ,
,  .
.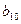
 .
.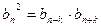 .
.


