МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ
I Дифференциальные уравнения Основные понятия и определения Обыкновенным дифференциальным уравнением называется уравнение F(x, y, y/, y//, …, y(n))=0, которое связывает независимый аргумент х, неизвестную функцию у и ее производные y, y/, y//, …, y(n). Порядком дифференциального уравнения называется максимальный порядок производной, входящей в уравнение. Решением дифференциального уравнения называется функция y = φ(x) которая при подстановке в уравнение превращает его в верное тождество. График этой функции называется интегральной кривой. Для дифференциального уравнения n–го порядка y(n) = f(x, y, y/, y//, …, y(n-1)) задача Коши формулируется следующим образом: для заданных начальных условий у0 = у(х0), Функция у = ψ(х, С1, С2, …, Сn), где С1, С2, …, Сn – произвольные постоянные, называется общим решением уравнения F(x, y, y/, y//, …, y(n))=0, если выполняются два условия: 1) для любых значений С1, С2, …, Сn функция у = ψ(х, С1, С2, …, Сn) является решением дифференциального уравнения F(x, y, y/, y//, …, y(n))=0; 2) для любой точки М0(х0, у0, Общее решение, записанное в неявном виде, называется общим интегралом. Если в общем решении у = ψ(х, С1, С2, …, Сn) зафиксированы константы С1, С2, …, Сn, то у = ψ(х, С1, С2, …, Сn) называется частным интегралом. Решить дифференциальное уравнение – значит найти его общее решение или общий интеграл.
|

 у/(х0), …,
у/(х0), …,  у(n-1)(х0) найти решение уравнения y(n) = f(x, y, y/, y//, …, y(n-1)), удовлетворяющее начальным условиям.
у(n-1)(х0) найти решение уравнения y(n) = f(x, y, y/, y//, …, y(n-1)), удовлетворяющее начальным условиям. ,
,  ,
, 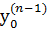 ) (n + 1)-мерного пространства существуют такие константы
) (n + 1)-мерного пространства существуют такие константы  ,
,  , …,
, …,  , при которых график решения у = ψ(х, С1, С2, …, Сn) проходит через точку М0(х0, у0,
, при которых график решения у = ψ(х, С1, С2, …, Сn) проходит через точку М0(х0, у0, 


