1. Ильин В.А., Позняк Э.Г. Линейная алгебра. М.: Наука, 1984. 340с.
2. Беклемишев Д.В. Курс аналитической геометрии и линей- ной алгебры. М.: Наука, 1987. 292с.
3. Бугров Я.С., Никольский С.М. Высшая математика. Элемен- ты линейной алгебры и аналитической геометрии. М.:Наука, 1980. 312с.
4. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. М.: Нау- ка, 1981. 207с.
5. Сборник задач по математике для ВТУЗов. Линейная алгебра и основы математического анализа, / Под ред. А.В. Ефимова, Б.П. Демидовича. М.: Наука, 1981. 464с.
СОДЕРЖАНИЕ
|
| Стр
|
| Глава I.
| Пределы
|
|
| Глава 2.
| Дифференциальное исчисление функций одной независимой переменной
|
|
|
| §1.
| Понятие производной
|
|
|
| §2.
| Основные правила дифференцирования. Дифференцирование основных элементарных функций.
|
|
|
| §3.
| Дифференцирование сложной функции
|
|
|
| §4.
| Производные высших порядков
|
|
|
| §5.
| Дифференциал функции
|
|
|
| §6.
| Применение производной при решении прикладных задач
|
|
| Глава 3.
| Исследование функций методами дифференциального исчисления
|
|
| §1.
| Интервалы монотонности функции
|
|
|
| §2.
| Экстремум функции
|
|
| Глава 4.
| Неопределенный интеграл
|
|
|
| §1.
| Непосредственное интегрирование
|
|
|
| §2.
| Интегрирование способом подстановки
(методом замены переменной)
|
|
|
| §3.
| Интегрирование по частям
|
|
|
| §4.
| Применение неопределенного интеграла при решении прикладных задач
|
|
| Глава 5.
| Определенный интеграл
|
|
|
| §1.
| Определенный интеграл и его непосредственное интегрирование
|
|
|
| §2.
| Приложение определенного интеграла для вычисления площадей плоских фигур
|
|
|
| §3.
| Приложение определенного интеграла к решению физических задач.
|
|
| Глава 6.
| Дифференциальные уравнения
|
|
|
| §1.
| Основные понятия
|
|
|
| §2.
| Уравнения с разделяющимися переменными
|
|
|
| §3.
| Однородные дифференциальные уравнения
|
|
|
| §4.
| Задачи на составление дифференциальных уравнений
|
|
| Глава 7.
| Элементы теории вероятностей и математической статистики
|
|
|
| §1.
| Основные понятия
|
|
|
| §2.
| Числовые характеристики распределения случайных величин
|
|
|
| §3.
| Нормальный закон распределения случайных величин
|
|
|
| §4.
| Генеральная совокупность. Оценка параметров генеральной совокупности по ее выборке
|
|
|
| §5.
| Интервальная оценка. Интервальная оценка при малой выборке. Распределение Стьюдента
|
|
|
| §6.
| Проверка гипотез. Критерии значимости.
|
|
|
| §7.
| Элементы корреляционного и регрессионного анализа.
|
|
|
|
| 7.1. Характер взаимосвязи между признаками
|
|
|
|
| 7.2. Проведение корреляционного анализа с помощью коэффициента парной корреляции
|
|
|
|
| 7.3. Элементы регрессионного анализа
|
|
| Лабораторные работы по статистической обработке результатов
|
|
|
| 1.
| Статистическая обработка данных измерения роста
|
|
|
| 2.
| Задания для проведения статистического анализа совокупности данных
|
|
| Приложение.
|
|
|
|
| П1.
| Правила приближенных вычислений
|
|
|
| П1.1
| Запись приближенных чисел
|
|
|
| П1.2.
| Правила округления
|
|
|
| П1.3.
| Вычисление с приближенными числами
|
|
| Ответы.
|
|
|
| Список литература
|
|
| | | | | |
«Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой»
Леонардо да Винчи,
G.36v (Записная книжка, 186 страница)
Глава 1
ПРЕДЕЛЫ
Постоянная  является пределом функции
является пределом функции  в точке
в точке  , если их разность во всех точках, кроме
, если их разность во всех точках, кроме  , по абсолютному значению остается меньше бесконечно малого положительного числа e.
, по абсолютному значению остается меньше бесконечно малого положительного числа e.
Если для  <e, то
<e, то  .
.
Практическое вычисление пределов основывается на следующих теоремах:
Если существуют  и
и 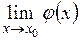 то
то
¯ 
 ±
± 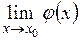
¯ 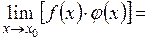
 ×
× 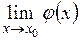
¯  (при
(при 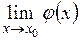 ≠0).
≠0).
Используют также следующие пределы:
 - первый замечательный предел
- первый замечательный предел
 - второй замечательный предел.
- второй замечательный предел.
Иногда в процессе отыскания предела при замене аргумента определенным значением функция получает выражение  или
или  - неопределенность. Хотя это выражение не имеет определенного смысла, функция может иметь конечный предел при данном стремлении аргумента. Это становится очевидным, если функцию преобразовать: разложить ее на множители, или поделить на аргумент, или умножить на сопряженное выражение, и т.д.
- неопределенность. Хотя это выражение не имеет определенного смысла, функция может иметь конечный предел при данном стремлении аргумента. Это становится очевидным, если функцию преобразовать: разложить ее на множители, или поделить на аргумент, или умножить на сопряженное выражение, и т.д.
Например:
ü  при замене
при замене  преобразовывается в неопределенность
преобразовывается в неопределенность  .
.
Раскрыть неопределенность можно, поделив все члены выражения, стоящего под знаком предела, на высшую степень аргумента, то есть на  :
:
 =
=  .
.
ü  - неопределенность.
- неопределенность.
Раскрыть данную неопределенность можно, разложив выражения, стоящие в числителе и знаменателе под знаком предела, на множители, то есть:


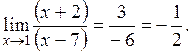
ü  - неопределенность.
- неопределенность.
Умножив и поделив выражение, стоящее под знаком предела, на сопряженное выражение  , получаем следующее выражение:
, получаем следующее выражение:

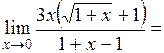
= 
 .
.
Найти следующие пределы:
1.1.  .
(Ответ: 3) .
(Ответ: 3)
| 1.6. 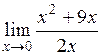 . (Ответ: 9/2) . (Ответ: 9/2)
|
1.2.  .
(Ответ: 1000) .
(Ответ: 1000)
| 1.7. 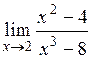 . (Ответ: 1/3) . (Ответ: 1/3)
|
1.3.  .
(Ответ: - .
(Ответ: -  ) )
| 1.8.  . (Ответ: . (Ответ:  ) )
|
1.4.  . (Ответ: . (Ответ: 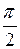 ) )
| 1.9.  . (Ответ: 1) . (Ответ: 1)
|
1.5.  . (Ответ: 0) . (Ответ: 0)
| 1.10.  . (Ответ: 4) . (Ответ: 4)
|
1.11.  . (Ответ: 0) . (Ответ: 0)
| 1.21.  . (Ответ: 1/2) . (Ответ: 1/2)
|
1.12.  . (Ответ: 0) . (Ответ: 0)
| 1.22 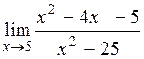 . (Ответ: 0,6) . (Ответ: 0,6)
|
1.13.  . (Ответ: 1/3) . (Ответ: 1/3)
| 1.23.  . (Ответ: 4) . (Ответ: 4)
|
1.14.  . (Ответ: 1/2) . (Ответ: 1/2)
| 1.24.  . (Ответ: 0) . (Ответ: 0)
|
1.15.  . (Ответ: 0) . (Ответ: 0)
| 1.25.  . (Ответ: 4) . (Ответ: 4)
|
1.16.  . (Ответ: 1/4) . (Ответ: 1/4)
| 1.26.  . (Ответ: e=2,718) . (Ответ: e=2,718)
|
1.17.  . (Ответ: . (Ответ:  ) )
| 1.27.  . (Ответ: 1) . (Ответ: 1)
|
1.18.  . (Ответ: 3) . (Ответ: 3)
| 1.28.  . (Ответ: e3) . (Ответ: e3)
|
1.19.  . (Ответ: 1) . (Ответ: 1)
| 1.29. 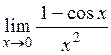 . (Ответ: 1/2) . (Ответ: 1/2)
|
1.20.  . (Ответ: 3) . (Ответ: 3)
| 1.30.  . (Ответ: 1/3) . (Ответ: 1/3)
|

 является пределом функции
является пределом функции  в точке
в точке  , если их разность во всех точках, кроме
, если их разность во всех точках, кроме  <e, то
<e, то  .
. и
и 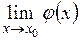 то
то
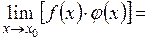
 (при
(при  - первый замечательный предел
- первый замечательный предел - второй замечательный предел.
- второй замечательный предел. или
или  - неопределенность. Хотя это выражение не имеет определенного смысла, функция может иметь конечный предел при данном стремлении аргумента. Это становится очевидным, если функцию преобразовать: разложить ее на множители, или поделить на аргумент, или умножить на сопряженное выражение, и т.д.
- неопределенность. Хотя это выражение не имеет определенного смысла, функция может иметь конечный предел при данном стремлении аргумента. Это становится очевидным, если функцию преобразовать: разложить ее на множители, или поделить на аргумент, или умножить на сопряженное выражение, и т.д. при замене
при замене  преобразовывается в неопределенность
преобразовывается в неопределенность  :
: .
. - неопределенность.
- неопределенность.

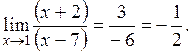
 - неопределенность.
- неопределенность. , получаем следующее выражение:
, получаем следующее выражение:
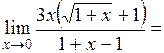

 .
. .
(Ответ: 3)
.
(Ответ: 3)
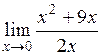 . (Ответ: 9/2)
. (Ответ: 9/2)
 .
(Ответ: 1000)
.
(Ответ: 1000)
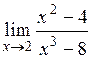 . (Ответ: 1/3)
. (Ответ: 1/3)
 .
(Ответ: -
.
(Ответ: -  )
)
 . (Ответ:
. (Ответ:  )
)
 . (Ответ:
. (Ответ: 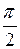 )
)
 . (Ответ: 1)
. (Ответ: 1)
 . (Ответ: 0)
. (Ответ: 0)
 . (Ответ: 4)
. (Ответ: 4)
 . (Ответ: 0)
. (Ответ: 0)
 . (Ответ: 1/2)
. (Ответ: 1/2)
 . (Ответ: 0)
. (Ответ: 0)
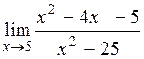 . (Ответ: 0,6)
. (Ответ: 0,6)
 . (Ответ: 1/3)
. (Ответ: 1/3)
 . (Ответ: 4)
. (Ответ: 4)
 . (Ответ: 1/2)
. (Ответ: 1/2)
 . (Ответ: 0)
. (Ответ: 0)
 . (Ответ: 0)
. (Ответ: 0)
 . (Ответ: 4)
. (Ответ: 4)
 . (Ответ: 1/4)
. (Ответ: 1/4)
 . (Ответ: e=2,718)
. (Ответ: e=2,718)
 . (Ответ:
. (Ответ:  )
)
 . (Ответ: 1)
. (Ответ: 1)
 . (Ответ: 3)
. (Ответ: 3)
 . (Ответ: e3)
. (Ответ: e3)
 . (Ответ: 1)
. (Ответ: 1)
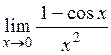 . (Ответ: 1/2)
. (Ответ: 1/2)
 . (Ответ: 3)
. (Ответ: 3)
 . (Ответ: 1/3)
. (Ответ: 1/3)



