Пример 9.
Установление степени влияния рекламных факторов на рекламный процесс. С помощью статистических методов изучения зависимостей можно установить, как проявляется теоретически возможная связь в данных конкретных условиях и какова количественная характеристика этой зависимости. Простейшим приемом обнаружения связи является сопоставление двух параллельных рядов- ряда значений факторного признака и соответствующих ему значений результативного признака. Результативный признак обозначается через а факторный через-x Например, маркетинговые исследования сети из 20 сбытовых предприятий показали затраты на рекламу и объем сбыта (таб. 1.10)
Таблица 1.10
Из общего анализа таблицы видно, что увеличение рекламы способствует увеличению объема продаж. Определим зависимость затрат на рекламу и величины сбыта в рекламной кампании. Построение корреляционной таблицы начинают с группировки значений факторного и результативного признаков. Для результативного признака необходимо определить величину интервала. Для этого воспользуемся формулой Стерджера: h=(y При формировании первого интервала от минимального значения следует отступить на половину длины интервала и далее формировать интервалы. В корреляционной таблице факторный признак располагается в строках, а результативный- в столбцах. Числа, расположенные на пересечении строк и столбцов, означают частоту повторения данного сочетания значения x и y (таб. 1.11)
Таблица 1.11
Где f Корреляционная таблица дает возможность выдвинуть предположение о наличии или отсутствии связи, а также выяснить её направление.если частоты в корреляционной таблице расположены по диагонали из левого верхнего угла в правый нижний угол (т.е. большим значениям фактора соответствует большие значения функции), то можно предположить наличие прямой корреляционной зависимости между признаками. Если же частоты расположены по диагонали справа налево, то предполагают наличие обратной связи между признаками. По данным таблицы 1.12 построим поле корреляции рассматриваемых факторов: Рис. 1.1. Поле корреляции
Характер распределения случайных величин на поле корреляции свидетельствует о наличии рассматриваемых связей. Итак, увеличение средних значений результативного признака с увеличением значении факторного признака ещё раз свидетельствует о возможном наличии прямой корреляционной зависимости объема сбыта от величины рекламы. Другим примером обнаружения связи является построение групповой таблицы. Все наблюдения разбиваются на группы в зависимости от величины признака – фактора, и по каждой группе вычисляются средние значения результативного признака (таб.1.12) Таблица 1.12.
Величина y Cравнив значение результативного признака по группам, можно сделать вывод, что увеличение рекламного бюджета способствует сбыту, что подтверждается прямой корреляционной зависимостью между признаками. Для выявления связи и её характера используют графический метод. Используя данные таблиц, строится в прямоугольных координатах точечный график, который называют «полем корреляции»(рис.1.2.)
Рис.1.2. Поле корреляции
Положение каждой точки на графике определяется величиной двух признаков - величиной рекламного бюджета и соответствующим ему объемом сбыта. Точки корреляционного поля не лежат на одной линии, они вытянуты определенной полосой слева направо. Имеющийся в нашем распоряжении статистический материал был сгруппирован, и по каждому значению рекламного бюджета определены значения среднего объема сбыта. Нанеся эти средние на график и соединяя последовательно отрезками прямых соответствующие им точки, получим так называемую эмпирическую линию связи. Если эмпирическая линия связи по своему виду приближается к прямой линии, то можно предположить наличие прямолинейной корреляционной связи между признаками. Если же имеется тенденция неравномерного изменения значений результативного признака, и эмпирическая линия связи будет приближаться к какой-либо кривой, то это может быть связано с наличием криволинейной связи. Показатели тесноты связи между признаками называют коэффициентами корреляции. Выявление связи между признаками осуществляется следующим образом: выдвигается нулевая статистическая гипотеза об отсутствии связи между признаками; рассчитывается соответствующий коэффициент корреляции k; проверяется, превосходит ли он некоторое критическое значение k> k Расчет линейного коэффициента для несгруппированных данных можно производить по формулам: 1)R= x и y –значения признаков, а 2)R= x и y –значения признаков, между которыми определяется коэффициент корреляции; n- объем выборки; 3)R= Линейный коэффициент корреляции |R|≤ 1Знак коэффициента характеризует направление взаимосвязи. Абсолютная величина R характеризует степень тесноты рассматриваемой взаимосвязи. Значимость линейного коэффициента корреляции определяется по таблицам критических значений R Например, используя данные таб 1 проведем расчет линейного коэффициента корреляции. Для I=20 величины ( Подставляя эти значения в выражение (2) получим R=0,9 Полученная величина линейного коэффициента корреляции свидетельствует о наличии тесной прямой связи между рассматриваемыми признаками. Знак при линейном коэффициенте корреляции указывает на направление связи –прямой зависимости соответствует знак плюс, обратной зависимости знак – минус. Квадрат коэффициента корреляции носит название коэффициента детерминации.Коэффициент детерминации можно считать определенным равенством R Для рассматриваемого примера с рекламным бюджетом, величина R
|





 ,например, для группы x=21 определится как y
,например, для группы x=21 определится как y  =(2*750+2*816+1*927)=973,8
=(2*750+2*816+1*927)=973,8



 . То гипотеза об отсутствии связи отвергается.
. То гипотеза об отсутствии связи отвергается. , где
, где и
и 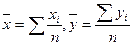 ),
), , где
, где
 , где а-уровень значимости (чаще всего 0,05), N-объем выборки. Линейный коэффициент корреляции может принимать значения от -1 до +1Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками. Можно воспользоваться упрощенным правилом: если |R|<0,3, то связь отсутствует; 0,3< |R|<0,5, то имеется связь слабая; если 0,5≤ |R|≤ 0,7, то связь достаточно сильная; если |R|≥ 0,7. то имеется высокая степень зависимости между признаками.
, где а-уровень значимости (чаще всего 0,05), N-объем выборки. Линейный коэффициент корреляции может принимать значения от -1 до +1Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками. Можно воспользоваться упрощенным правилом: если |R|<0,3, то связь отсутствует; 0,3< |R|<0,5, то имеется связь слабая; если 0,5≤ |R|≤ 0,7, то связь достаточно сильная; если |R|≥ 0,7. то имеется высокая степень зависимости между признаками. =178300,
=178300,  =439,
=439, 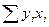 =394680,
=394680, ,(
,(


 =
= 



