Пример 16
Оценка выбора рекламных стратегий. На рекламном рынке происходит игра между рекламодателем (РД) и рекламным агентством (РА),которую можно формализовать матрицей рекламных платежей А B ………………………
Где a Стратегии РД= (B1,B2,…,Bn) -это признаки желательности (узнаваемость торговой марки, благоприятный образ, увеличение сбыта и т.д.) или общие стратегии рекламы в зависимости от жизненного цикла товара, ситуации на рынке и т.д., которые РД пытается получить от вложения своих средств в рекламу, представляемую в стратегиях Ai Предположим, что значения a Цель РА- максимизировать заказы, цель РД- минимизировать рекламные затраты. В этом заключается смысл игры субъектов рекламного рынка Пусть матрица А не содержит седловой точки, т.е. игра решается в смешанных стратегиях: S*1=(p Таким образом, задача решения игры на рекламном рынке сводится к задаче линейного программирования. оптимальные стратегии S*1 S*2 с матрицей рекламных платежей A
Решая их, находим значения X Рассмотрим следующий конкретный пример. Найти решение игры между РД и РА,исходя из значений рекламных платежей в тыс.руб. или у.е. А= Постановка математической модели пары двойственных задач линейного программирования для матрицы А будет выглядеть так: Найти минимум функции F(X)= X1+X2+X3 при ограничениях:
X Решая систему уравнений (1) находим корни:X1= Задача нахождения оптимальной стратегии РД формулируется следующим образом: Найти максимум функции F(Y)=Y
Y Так как Y
q Решая систему уравнений, находим значения корней: q Таким образом, оптимальная стратегия РД будет: S*2=( Данный метод линейного программирования позволяет принимать оптимальные стратегии пары игроков –РД и РА на рекламном рынке, что сокращает рекламные издержки при решении требуемой стратегии рекламодателя. Рассмотрим конкретный пример. Выделенный объем рекламного бюджета РД составляет 1000$. Требуется определить объем рекламы по каждому из её видов и гарантированный уровень сбыта рекламируемого товара. Известно, если реклама вида j(1≤ j ≤ n) будет эффективна, то при сбыте РД получит прибыль d M
H= Предположим, что доходы от продаж по каждому виду рекламы равны, т.е. d1=d2=…=dn=d Например, известны данные по рекламным затратам и ожидаемый доход, отраженный в таблице: Таблица 1.19.
С учетом этих данных матрица выигрышей будет иметь следующий вид:
H= Преобразуем эту матрицу путем вычитания из каждого элемента d=10 к виду:
H= Проверим условие рентабельности сбыта от действия рекламы: R= В нашем случае это условие R= Правильная рекламная политика наблюдается при смешанной стратегии S Для стратегии 1 величина P Ожидаемый доход (D) РД будет равен значению игры, которое определяется по формуле: D= В рассмотренном случае ожидаемый доход отрицателен. Следовательно, необходимо выбрать другую рекламную стратегию и провести аналогичное исследование, пока не будет достигнут положительный результат. Таким образом, при использовании смешанной стратегии, т.е. применения различного вида рекламы, доход гарантируется лишь в среднем, является ожидаемым и не может совпадать точно с реальным выигрышем, что и является характерным в условиях риска.
|

 :
: B
B  …. B
…. B 

 –выигрыш, а точнее, рекламные затраты, планируемые РА в ситуациях, когда РА выбрала рекламную стратегию А
–выигрыш, а точнее, рекламные затраты, планируемые РА в ситуациях, когда РА выбрала рекламную стратегию А  В общем случае у РА= (A1,A2,…,Am) Под рекламной стратегией может быть представлен выбираемый тип, вид рекламы, какие-то рекламные услуги, эффективность рекламной кампании, величина рекламного бюджета общие стратегии и т.п.
В общем случае у РА= (A1,A2,…,Am) Под рекламной стратегией может быть представлен выбираемый тип, вид рекламы, какие-то рекламные услуги, эффективность рекламной кампании, величина рекламного бюджета общие стратегии и т.п. , где p
, где p  -вероятности использования РА стратегий A1,A2,…,A
-вероятности использования РА стратегий A1,A2,…,A  - вероятность использования РД рекламных стратегий B1,B2,…Bn(
- вероятность использования РД рекламных стратегий B1,B2,…Bn( .
.
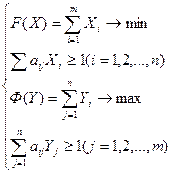
 Y
Y  цену
цену  игры и оптимальные стратегии S*1 S*2, где
игры и оптимальные стратегии S*1 S*2, где  (i=1,2,…,m) q
(i=1,2,…,m) q 



 Из
Из  находим
находим 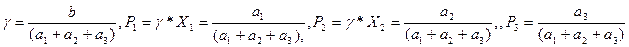 ,где a
,где a  - числа из корней решения уравнения. Таким образом, оптимальная стратегия РА будет S*1=(
- числа из корней решения уравнения. Таким образом, оптимальная стратегия РА будет S*1=( ,где с = a
,где с = a 
 при ограничениях
при ограничениях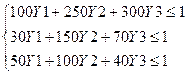

 ,то сиcтему уравнений можно переписать так:
,то сиcтему уравнений можно переписать так:
 , q
, q  ,q
,q  ,Y
,Y  =
= 
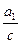 ,
, 
 )
)

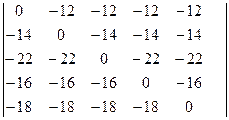
 >0
>0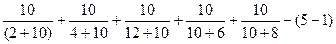 >0
>0 , где вероятности p
, где вероятности p  Где 1
Где 1 
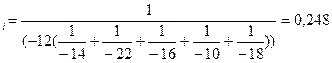 аналогично определяем остальные доли деления рекламного бюджета по видам рекламы. Смешанная стратегия запишется как S
аналогично определяем остальные доли деления рекламного бюджета по видам рекламы. Смешанная стратегия запишется как S  , согласно которой бюджет вQ=1000у.е. следует разделить на объемы по видам рекламы: Q1=248у.е., Q2=210 у.е.,Q3=122 у.е.,Q4=175 у.е.,Q5=244
, согласно которой бюджет вQ=1000у.е. следует разделить на объемы по видам рекламы: Q1=248у.е., Q2=210 у.е.,Q3=122 у.е.,Q4=175 у.е.,Q5=244



