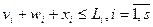Моделирование распределения усилий в рекламной деятельности
Рекламная деятельность - это многогранная циклическая деятельность рекламодателя для решения задачи: как минимальным рекламным бюджетом достичь максимальной действенности рекламы; как оптимально распределить ресурсы рекламы для получения максимальной эффективности рекламной кампании. Основная цель управления рекламной деятельностью – это достижение наибольшей отдачи от затрат на рекламу при минимизации последних В этом направлении рассмотрим моделирование нескольких прикладных задач путем динамического программирования.
В рекламной деятельности стоит задача: необходимо распространить N единиц рекламной продукции какого-либо одного средства рекламы по S районам, в которых проживают потенциальные потребители, различающиеся своим потребительским поведением. Из проведенных маркетинговых исследований известно, что если направить x  рекламной продукции в район I, то действенность (D) или эффективность рекламы составит D
рекламной продукции в район I, то действенность (D) или эффективность рекламы составит D 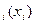 .Цель рекламодателя состоит в нахождении такого плана распределения N единиц рекламы по M=1,2,…,m районам, чтобы получить максимальную действенность рекламы.Действенность рекламы может выражаться в объемах продаж, увеличении числа посетителей рекламируемого магазина, увеличении числа повторных покупок или в проценте информированных о товаре через рекламу. В такой постановке задача ограничивается одним средством рекламы, например, распространением печатной рекламы по спальным районам, рекламы по кабельном каналу, щитовая реклама на улицах и т.д.
.Цель рекламодателя состоит в нахождении такого плана распределения N единиц рекламы по M=1,2,…,m районам, чтобы получить максимальную действенность рекламы.Действенность рекламы может выражаться в объемах продаж, увеличении числа посетителей рекламируемого магазина, увеличении числа повторных покупок или в проценте информированных о товаре через рекламу. В такой постановке задача ограничивается одним средством рекламы, например, распространением печатной рекламы по спальным районам, рекламы по кабельном каналу, щитовая реклама на улицах и т.д.
В такой постановке задача классического динамического программирования примет вид:
 при ограничениях
при ограничениях 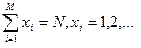
Примем d  -действенность рекламы при оптимальном распределении n единиц из N по районам 1,2,…,i,x
-действенность рекламы при оптимальном распределении n единиц из N по районам 1,2,…,i,x  -количество рекламы, направленной на район i и создающей действенность d
-количество рекламы, направленной на район i и создающей действенность d  Тогда рекуррентное соотношение динамического программирования запишется в виде:
Тогда рекуррентное соотношение динамического программирования запишется в виде:
d 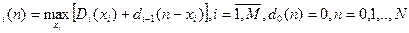
Максимум функции d  берется только по неотрицательным целочисленным значениям x
берется только по неотрицательным целочисленным значениям x  , удовлетворяющим условию x
, удовлетворяющим условию x  .
.
При известных значениях функции действенности рекламы D 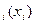 и N вычисления при решении задачи начинают с определения значений d
и N вычисления при решении задачи начинают с определения значений d  при i=1.Затем вычисляются значения d
при i=1.Затем вычисляются значения d  и так последовательно до значения d
и так последовательно до значения d 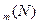 .Оптимальное распределение находится путем осуществляемое в обратном порядке выбора значений x
.Оптимальное распределение находится путем осуществляемое в обратном порядке выбора значений x  , дающих в совокупности d
, дающих в совокупности d  .
.
Рассмотрим модель общего вида в распределении рекламных усилий при нелинейном ограничении r 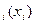 - i-ое средство рекламы (носитель рекламы, медиаканал и т.д.), состоящее из x
- i-ое средство рекламы (носитель рекламы, медиаканал и т.д.), состоящее из x  единиц рекламной продукции. Она по аналогии с вышерассмотренной запишется в виде:
единиц рекламной продукции. Она по аналогии с вышерассмотренной запишется в виде:
 при
при  где x
где x  при любом i.
при любом i.
Из постановки задачи следует, что r 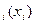 –неубывающая функция, удовлетворяющая условию r
–неубывающая функция, удовлетворяющая условию r  Для упрощения решения примем, что r
Для упрощения решения примем, что r 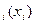 =x
=x  вследствие чего допустимое решение существует при любом значении N. Тогда рекуррентное соотношение динамического программирования примет вид:
вследствие чего допустимое решение существует при любом значении N. Тогда рекуррентное соотношение динамического программирования примет вид:
d  (n)=
(n)= 
 ,i=
,i=  при i=0,n=0,1,…,N,r
при i=0,n=0,1,…,N,r 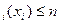
В оптимизационной задаче отыскивается значение d  путем последовательного вычисления значений каждой функции d
путем последовательного вычисления значений каждой функции d  при n =0,1,…,N Начиная с i=1 до i=S.
при n =0,1,…,N Начиная с i=1 до i=S.
Рассмотрим задачу распределения усилий с двумя ограничениями. Рекламодатель планирует проведение рекламной кампании в одном из районов по определенному медиаканалу. В районе имеется S рекламоносителей. Для каждого i рекламоносителя известна действенность рекламы D 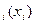 , как чистый доход с вычетом расходов на рекламу с выделенной суммой x
, как чистый доход с вычетом расходов на рекламу с выделенной суммой x  денег рекламного бюджета на оплату медиаканалу. Величина рекламного бюджета составляет N денежных единиц. Рекламодатель установил, что количество показов рекламного сообщения в течение дня не должно превышать числа M. Медиаканал i согласен осуществить показ K
денег рекламного бюджета на оплату медиаканалу. Величина рекламного бюджета составляет N денежных единиц. Рекламодатель установил, что количество показов рекламного сообщения в течение дня не должно превышать числа M. Медиаканал i согласен осуществить показ K 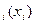 рекламы за сумму x
рекламы за сумму x  денег. Оптимизационная модель задачи запишется в виде
денег. Оптимизационная модель задачи запишется в виде
 при ограничениях
при ограничениях
 (общая сумма рекламного бюджета) x
(общая сумма рекламного бюджета) x  при любом i
при любом i
 (число показов рекламы за день)
(число показов рекламы за день)
Соответствующее задаче рекуррентное соотношение будет иметь вид
d 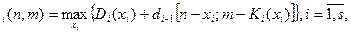
где n=0,1,…,N,m=0,1,…,M, x 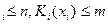
Функция d  представляет собой доход от оптимального распределения рекламного бюджета по медиаканалам в зависимости от частоты показов рекламы в день. Задача решается аналогично ранее рассмотренной.
представляет собой доход от оптимального распределения рекламного бюджета по медиаканалам в зависимости от частоты показов рекламы в день. Задача решается аналогично ранее рассмотренной.
Аналогичная постановка задачи с двумя ограничениями состоит в следующем. Рекламодатель рассматривает распределение рекламного бюджета по s средствам рекламы или медиаканалам. Для осуществления варианта I  требуется выделить сумму в K
требуется выделить сумму в K  денежных единиц из рекламного бюджета. Величина рекламного бюджета составляет М, и она строго фиксирована Действенность рекламы от вложений по i-м варианту составляет D
денежных единиц из рекламного бюджета. Величина рекламного бюджета составляет М, и она строго фиксирована Действенность рекламы от вложений по i-м варианту составляет D  единиц. Рекламодатель стремится максимизировать действенность рекламы по s медиаканалам. Рекламодатель принимает решение, что количество медиаканалов не должно превышать величины N. Каждый вариант решения уникален и нужно решить, принимать его или отвергнуть в данной рекламной кампании.
единиц. Рекламодатель стремится максимизировать действенность рекламы по s медиаканалам. Рекламодатель принимает решение, что количество медиаканалов не должно превышать величины N. Каждый вариант решения уникален и нужно решить, принимать его или отвергнуть в данной рекламной кампании.
Примем, что переменная x  , сопоставляемая i–у варианту, может принимать только значения: x
, сопоставляемая i–у варианту, может принимать только значения: x  (вариант отвергнуть) или x
(вариант отвергнуть) или x  (вариант принять).Перечисленные условия запишутся в виде следующей модели.
(вариант принять).Перечисленные условия запишутся в виде следующей модели.
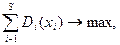
При ограничениях  (число медиаканалов), x
(число медиаканалов), x  при любом i
при любом i
 (объем рекламного бюджета), x
(объем рекламного бюджета), x  при любом i
при любом i
В этой задаче d  есть доход рекламодателя от оптимального распределения m единиц рекламного бюджета по n медиаканалам, выбранным из варианта1,2,…,
есть доход рекламодателя от оптимального распределения m единиц рекламного бюджета по n медиаканалам, выбранным из варианта1,2,…,
Рассмотрим другой класс задач в распределении рекламных усилий. Рекламодатель планирует поделить рекламный бюджет между s медиаканалами. Для каждого медиаканала в планировании рекламного бюджета имеется деление бюджета на три составляющие.Отчисления первой группы соответствуют исследованиям рекламы, т.е. на i–й медиаканал на его рекламные исследования выделяется v  средств бюджета с ожидаемой действенностью рекламы от этого этапа P
средств бюджета с ожидаемой действенностью рекламы от этого этапа P  денежных единиц. Отчисления второй группы представляют затраты на апробацию рекламы на фокус-группе по i-му медиаканалу. На второй этап выделяется w
денежных единиц. Отчисления второй группы представляют затраты на апробацию рекламы на фокус-группе по i-му медиаканалу. На второй этап выделяется w  средств бюджета, что может принести в будущем доход рекламодателю в размере Q
средств бюджета, что может принести в будущем доход рекламодателю в размере Q  .К третьей группе относят затраты, связанные с показом рекламы по медиаканалу. Затраты третьей группы x
.К третьей группе относят затраты, связанные с показом рекламы по медиаканалу. Затраты третьей группы x  должны принести D
должны принести D 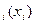 дохода от рекламы по i-му медиаканалу.
дохода от рекламы по i-му медиаканалу.
Общая сумма маркетинговых отчислений на рекламу (рекламный бюджет) составляет N.Однако, директор по маркетингу может установить верхний предел L  отчислений рекламного бюджета на i-й медиаканал. Задача менеджера по рекламе состоит в распределении рекламного бюджета таким образом, чтобы обеспечивать максимизацию общего дохода рекламодателя при наложенных ограничениях.
отчислений рекламного бюджета на i-й медиаканал. Задача менеджера по рекламе состоит в распределении рекламного бюджета таким образом, чтобы обеспечивать максимизацию общего дохода рекламодателя при наложенных ограничениях.
Математическая модель задачи описывается следующими соотношениями:

 при ограничениях
при ограничениях

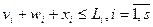
Рекуррентное отношение для данной задачи запишется в виде,
Где максимизация должна удовлетворить условию, тогда эту задачу также можно решить методом перебора.
Таким образом, используя динамические модели распределения рекламных усилий, можно повысить рентабельность рекламной деятельности, сократить время на обдумывания множества вариантов решений, улучшить технологию принятия решений, принять оптимальные решения.

 рекламной продукции в район I, то действенность (D) или эффективность рекламы составит D
рекламной продукции в район I, то действенность (D) или эффективность рекламы составит D 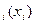 .Цель рекламодателя состоит в нахождении такого плана распределения N единиц рекламы по M=1,2,…,m районам, чтобы получить максимальную действенность рекламы.Действенность рекламы может выражаться в объемах продаж, увеличении числа посетителей рекламируемого магазина, увеличении числа повторных покупок или в проценте информированных о товаре через рекламу. В такой постановке задача ограничивается одним средством рекламы, например, распространением печатной рекламы по спальным районам, рекламы по кабельном каналу, щитовая реклама на улицах и т.д.
.Цель рекламодателя состоит в нахождении такого плана распределения N единиц рекламы по M=1,2,…,m районам, чтобы получить максимальную действенность рекламы.Действенность рекламы может выражаться в объемах продаж, увеличении числа посетителей рекламируемого магазина, увеличении числа повторных покупок или в проценте информированных о товаре через рекламу. В такой постановке задача ограничивается одним средством рекламы, например, распространением печатной рекламы по спальным районам, рекламы по кабельном каналу, щитовая реклама на улицах и т.д. при ограничениях
при ограничениях 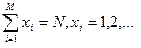
 -действенность рекламы при оптимальном распределении n единиц из N по районам 1,2,…,i,x
-действенность рекламы при оптимальном распределении n единиц из N по районам 1,2,…,i,x 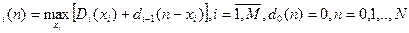
 .
. при i=1.Затем вычисляются значения d
при i=1.Затем вычисляются значения d  и так последовательно до значения d
и так последовательно до значения d 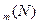 .Оптимальное распределение находится путем осуществляемое в обратном порядке выбора значений x
.Оптимальное распределение находится путем осуществляемое в обратном порядке выбора значений x  .
. где x
где x  при любом i.
при любом i. Для упрощения решения примем, что r
Для упрощения решения примем, что r  вследствие чего допустимое решение существует при любом значении N. Тогда рекуррентное соотношение динамического программирования примет вид:
вследствие чего допустимое решение существует при любом значении N. Тогда рекуррентное соотношение динамического программирования примет вид: (n)=
(n)= 
 ,i=
,i=  при i=0,n=0,1,…,N,r
при i=0,n=0,1,…,N,r 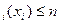
 при ограничениях
при ограничениях (общая сумма рекламного бюджета) x
(общая сумма рекламного бюджета) x  (число показов рекламы за день)
(число показов рекламы за день)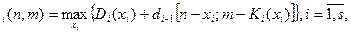
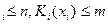
 представляет собой доход от оптимального распределения рекламного бюджета по медиаканалам в зависимости от частоты показов рекламы в день. Задача решается аналогично ранее рассмотренной.
представляет собой доход от оптимального распределения рекламного бюджета по медиаканалам в зависимости от частоты показов рекламы в день. Задача решается аналогично ранее рассмотренной. требуется выделить сумму в K
требуется выделить сумму в K  (вариант отвергнуть) или x
(вариант отвергнуть) или x  (вариант принять).Перечисленные условия запишутся в виде следующей модели.
(вариант принять).Перечисленные условия запишутся в виде следующей модели.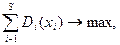
 при любом i
при любом i денежных единиц. Отчисления второй группы представляют затраты на апробацию рекламы на фокус-группе по i-му медиаканалу. На второй этап выделяется w
денежных единиц. Отчисления второй группы представляют затраты на апробацию рекламы на фокус-группе по i-му медиаканалу. На второй этап выделяется w 
 при ограничениях
при ограничениях