Пример 17. Выбор рекламных стратегий по моделям игровых задач.
Выбор рекламных стратегий по моделям игровых задач. Известно достаточно много рекламных стратегий, используемых рекламодателем для продвижения своих товаров. Однако, используются стратегии рекламодателем интуитивно или неоптимально, в смысле рекламных издержек. Стоит задача в формализации принимаемых рекламных стратегий и их оптимизации по критерию издержек. Рассмотрим следующую ситуацию: Рекламное агентство (РА) разработала для рекламодателя (РД) – m стратегий по видам предлагаемой рекламы для продвижения её товара на рынке. Каждая стратегия i характеризуется величиной рекламных затрат А Пусть каждая сторона выбрала определенную стратегию, РА-А Пусть a Предположим, что значения a Составим прямоугольную таблицу, строки которой соответствуют стратегии РФ, а столбцы – РД. Эта таблица называется платежной матрицей. Каждый элемент a
Таблица 1.20
В качестве A 1) наиболее выгодной стратегии РА из стратегий A 2) наилучшей (оптимальной) стратегии РД из набора B При условии, что РА и РД делают все для того, чтобы добиться своей цели. Если РА выбирает стратегию А Если РФ выбирает стратегию A Выбирая стратегию A а=max a Величина а- гарантированный выигрыш, который обеспечивает себе РА при любой стратегии поведения РД. РД заинтересован в том, чтобы уменьшить свой проигрыш в финансировании рекламы, т.е обратить выигрыш РА в минимум. Для выбора оптимальной стратегии РФ должна найти максимальное значение выигрыша в каждом столбце и среди этих значений выбрать наименьшее. Обозначим через b b= Стратегия РД, обеспечивающая получение верхней цены игры, называется минимаксной чистой стратегией x Применяя её, РД проиграет не больше b при любых предложениях от РФ: b Например, из представленной ниже матрицы рекламных затрат определим нижнюю и верхнюю цены игры и минимаксные стратегии: Таблица 1.21
Из матрицы находим Таким образом, нижней цене игры (а=20)соответствует стратегия РФ-А Верхней цене игры b=22тыс.руб. соответствует стратегия РД- B Существуют ситуации на рекламном рынке, для которых нижняя цена игры равна верхней, т.е. a=b. Такие ситуации называются играми с седловой точкой, в этом случае a=b= Например, дана матрица платежей за рекламу: Таблица 1.22.
Откуда a=max(10,22,7)=22; b=min (25,30,40,22) Следовательно, a=b=22, тогда cедловой точкой (оптимальной стратегией РА и РД) является пара A Рассмотрим игровые ситуации на рекламном рынке в смешанных стратегиях. Для применения смешанных стратегий требуются следующие условия: в игре отсутствует седловая точка; игроками (РА и РД) используются случайная смесь стратегий с соответствующими вероятностями; игра многократно повторяется в одних и тех же условиях; при каждом из ходов РА и РД не информированы о выборе стратегии; допускается усреднение результатов игровой ситуации. Смешанные стратегии игроков –РФ и РД, применяющих соответственно стратегии A Смешанную стратегию для РА-S S Для рекламодателя (РД) как S
Матрица платежей за рекламу запишется так: A Зная матрицу А можно определить средний выигрыш (математическое ожидание) M(A РА, применяя смешанные стратегии, стремится увеличить свой выигрыш (получить большой заказ на рекламу), достигая а= РД добивается, чтобы а= Обозначим через p*
При этом выполняется условие: M(A,p,q* Решить игру- означает найти цену рыночной игры и оптимальные стратегии.Следует заметить, что каждая рыночная конечная игра имеет цену j,т.е.j – средний выигрыш, приходящийся на одну партию, удовлетворяющую условию a Таким образом, имеются матрицы S p* Из условий следует, каковы бы ни были действия РА и РД, выигрыш будет равен цене игры -
p Для РД система уравнений будет аналогична:
q Решая системы уравнений для РД и РА находим оптимальные решения: S A= Так как a=16, b=20, то a Для РА:
p Для РД:
q Решая системы уравнений, находим: p S
|

 , тогда набор рекламных стратегий от рекламного агентства запишется так РА=(A1,A2,…,An) Рекламодатель РД имеет также несколько(n) стратегий РД=(B1,B2,…,Bn), которые он желает получить от действия своих средств, вложенных в рекламу.
, тогда набор рекламных стратегий от рекламного агентства запишется так РА=(A1,A2,…,An) Рекламодатель РД имеет также несколько(n) стратегий РД=(B1,B2,…,Bn), которые он желает получить от действия своих средств, вложенных в рекламу. такое действие называется матричной игрой размерностью mxn.
такое действие называется матричной игрой размерностью mxn. –выигрыш РА в ситуации, когда РА выбрала рекламную стратегию A
–выигрыш РА в ситуации, когда РА выбрала рекламную стратегию A  .Выигрыш РД в данной ситуации обозначим через b
.Выигрыш РД в данной ситуации обозначим через b  для любых i и j.
для любых i и j. .
.



































 может выступать комбинация (сочетание) одновременно предлагаемых видов рекламы для получения комбинации B
может выступать комбинация (сочетание) одновременно предлагаемых видов рекламы для получения комбинации B  желаемых стратегий РД. Задача состоит в определении:
желаемых стратегий РД. Задача состоит в определении: ;
; ;
; , т.е. a
, т.е. a  , т.е. a
, т.е. a  Наименьшее значение b
Наименьшее значение b 
 Таким образом, РА желает получить выигрыш не менее а независимо от действий РД, а РД гарантирует себе проигрыш не больше b.
Таким образом, РА желает получить выигрыш не менее а независимо от действий РД, а РД гарантирует себе проигрыш не больше b. -Цели РД
-Цели РД
 -вид рекламоносителя
-вид рекламоносителя

 тыс.руб.
тыс.руб. называется чистой ценой игры ¸а стратегия игроков рФ и РД –Ai
называется чистой ценой игры ¸а стратегия игроков рФ и РД –Ai  Bj оптимальными. Пара (Ai,Bj) называется cедловой точкой матрицы, т.к. элемент a
Bj оптимальными. Пара (Ai,Bj) называется cедловой точкой матрицы, т.к. элемент a 
 , S
, S  где p
где p  –вероятности использования РФ стратегий A
–вероятности использования РФ стратегий A  - вероятность использования РД рекламных стратегий B
- вероятность использования РД рекламных стратегий B 






 и q*
и q*  векторы, соответствующие оптимальным смешанным стратегиям РА и РД, при которых выполняется равенство:
векторы, соответствующие оптимальным смешанным стратегиям РА и РД, при которых выполняется равенство: =
= 

 .Каждый из игроков –РА и РД при многократном повторении игры получает более выгодный для себя результат.
.Каждый из игроков –РА и РД при многократном повторении игры получает более выгодный для себя результат. .Требуется найти оптимальные смешанные стратегии РФ и РД, т.е. S
.Требуется найти оптимальные смешанные стратегии РФ и РД, т.е. S  и цену рыночной игры-
и цену рыночной игры-  q*
q* 




 и
и 
 и решение ищем в смешанных стратегиях. Системы уравнений имеют вид:
и решение ищем в смешанных стратегиях. Системы уравнений имеют вид:
 >1
>1
 =1
=1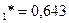 ; p*
; p*  ;q
;q  ; q
; q  ;
;  .Следовательно, оптимальные стратегии для субъектов рекламного рынка
.Следовательно, оптимальные стратегии для субъектов рекламного рынка с выигрышем (заказом на рекламу) 18,57 у.е.
с выигрышем (заказом на рекламу) 18,57 у.е.


