Пример 1. Возьмем конкретные данные о затратах на стимулирование продаж по месяцам (Табл.2.1) и построим для них линейную модель.
Возьмем конкретные данные о затратах на стимулирование продаж по месяцам (Табл.2.1) и построим для них линейную модель. Решение. В табл. 2.1 приведены промежуточные вычисления и результаты использования линейной модели. В нижней строке записаны суммы значений в колонках. Таблица 2.1
Исходя из первых двух, легко определить: Параметры линейного уравнения рассчитаем по формулам:
где tcp – среднее значение фактора времени; ycp – среднее значение исследуемого показателя. Подставляя рассчитанные значения в вышеприведенную формулу, получаем:
Таким образом линейная модель имеет вид:
Последовательно подставляя в модель вместо фактора t его значения от 1 до N, получаем расчетные значения уровней yp:
Вычислим отклонения расчетных значений от фактических наблюдений
Отражает ли эта модель закономерность изменения исследуемого показателя, иными словами можно ли полученные значения yp рассматривать как тенденцию? Для ответа на этот вопрос оценим качество модели, или ее адекватность исследуемому процессу. Последняя характеризуется выполнением определенных статистических свойств и точностью, т. е. степенью близости к фактическим данным. Модель считается хорошей со статистической точки зрения, если она адекватна и достаточно точна. Модель является адекватной, если математическое ожидание значений остаточного ряда близко или равно нулю, и если значения остаточного ряда случайны, независимы и подчинены нормальному закону распределения. Результаты исследования (оценка) адекватности вышеприведенной модели отражены в табл. 2.2. Таблица 2.2
1. Проверка равенства математического ожидания уровней ряда остатков нулю осуществляется с использованием t-критерия Стьюдента:
где SЕ — среднее квадратическое отклонение уровней остаточного ряда. Значение
Если
Гипотеза отклоняется, если t > t табл с заданным уровнем доверительной вероятности р. При N = 9 и р = 70% t табл. = 1,05 В рассматриваемом примере 2. Проверку случайности уровней ряда остатков проведем на основе критерия поворотных точек. В соответствии с ним каждый уровень ряда сравнивается с двумя рядом стоящими. Если он больше или меньше их, то эта точка считается поворотной. Далее подсчитывается сумма поворотных точек " р ". В случайном ряду чисел должно выполняться строгое неравенство:
Квадратные скобки здесь означают, что от результата вычислений берется целая часть числа. При N = 9 в правой части неравенства имеем:
В табл. 2.2.2. в третьей графе для первого и последнего наблюдения проставим прочерк, ноль — если точка неповоротная, и единицу, если она поворотная. В нашем примере количество поворотных точек равно трем (р= =3), неравенство (2.10) выполняется, следовательно, свойство случайности выполняется. 3. При проверке независимости (отсутствия автокорреляции) опреде-ляется отсутствие в ряду остатков систематической составляющей. Это проверяется с помощью d-критерия Дарбина-Уотсона, в соответствии с которым вычисляется коэффициент d
Вычисленная величина этого критерия сравнивается с двумя табличными уровнями (нижним d1 и верхним d2). Если d находится в интервале от нуля до d1, то уровни ряда остатков сильно автокоррелированы, а модель неадекватна. Если его значение попадает в интервал от d2 до 2, то уровни ряда являются независимыми. Если d превышает 2, то это свидетельствует об отрицательной корреляции и перед вводом в таблицу его величину надо преобразовать:
Для линейной модели при 9 наблюдениях можно взять в качестве критических табличных уровней величины d1=1,08 и d2=1,36 (см. Приложение 2). Следовательно, расчетное значение d попало в зону между d1 и d2, поэтому однозначного вывода сделать нельзя и необходимо применение других критериев, например, первого коэффициента автокорреляции, который вычисляется по формуле
Если |r1| > rтабл . (при N < 15, r табл = 0,36), то присутствие в остаточном ряду существенной автокорреляции подтверждается. Для рассматриваемого примера r1 = 7,60: 48,82 = 0,16. Следовательно, по этому критерию выполняется свойство независимости уровней остаточной компоненты. 4. Соответствие ряда остатков нормальному закону распределения определим при помощи RS-критерия
где Emax — максимальный уровень ряда остатков; Emin — минимальный уровень ряда остатков; SE — среднее квадратическое отклонение. Если значение этого критерия попадает между табулированными границами с заданным уровнем вероятности, то гипотеза о нормальном распределении ряда остатков принимается. Для N = 10 и 5%-ного уровня значимости этот интервал равен (2,7—3,7)(см. Приложение 2). В нашем примере: Еmах - 3,9 и Еmin = -3,5, а размах 7,4.
Расчетное значение попадает в интервал. Следовательно, свойство нормальности распределения выполняется, что позволяет строить доверительный интервал прогноза. Для характеристики точности воспользуемся средней относительной ошибкой:
Величина менее 5 % свидетельствует о хорошем уровне точности модели (ошибка до 15 % считается приемлемой). Точечный прогноз на k шагов вперед получается путем подстановки в модель параметра t = N + 1,..., N + k. При прогнозировании на два шага имеем:
Доверительный интервал прогноза будет иметь следующие границы: Верхняя граница прогноза = Нижняя граница прогноза = Величина Uk для линейной модели имеет вид:
где ST — среднее квадратическое отклонение от линии тренда. Если в качестве линии тренда используется уравнение прямой, то:
Для нашего примера
Коэффициент kр является табличным значением t-статистики Стьюдента. Если исследователь задает уровень вероятности попадания прогнозируемой величины внутрь доверительного интервала равный 70 %, то kр = 1,05, и, следовательно:
В табл. 2.6 сведены результаты расчетов прогнозных оценок по линейной модели по формуле (2.3.). Таблица 2.3.
Если построенная модель адекватна, то с выбранной пользователем вероятностью можно утверждать, что при сохранении сложившихся закономерностей развития, прогнозируемая величина попадает в интервал, образованный нижней и верхней границами. В нашем случае модель полностью адекватна исследуемому процессу и, следовательно, такое утверждение правомерно.
|

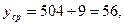
 .
. ,
,
 ,
, .
.
 .
. ,
, .
. :
: ,
, и т.д.
и т.д.
 .
. — среднее значение уровней остаточного ряда;
— среднее значение уровней остаточного ряда; ,
,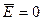 ,то
,то .
. .
.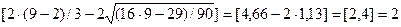 .
. .
. . В нашем примере
. В нашем примере  .
.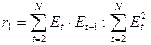 .
. .
.
 .
.
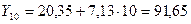 ,
, .
.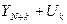 ,
,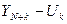 .
.
 или
или  .
. .
. ,
, .
.


