Пример 15. Необходимо принять решение для финансирования двух видов рекламы: X -реклама в газете1 и X –реклама в газете 2
Необходимо принять решение для финансирования двух видов рекламы: X Таблица 1.18
По данным приведенной таблицы экономико-математическая задача линейного программирования формулируется следующим образом. Найти значения покупок рекламы по величине рекламных блоков в газетах 1 и2 при условии минимума функции Z=6X
Ограничивающие соотношения суть неравенство, выражающее требование, чтобы реклама воздействовала в соответствии с принятой нормой. Таким образом, в задаче требуется минимизировать функцию Z. Например, можно определить минимум Z при условии выполнения одного ограничения X Z=6X и минимум выражения Z получится при X При таком решении достигается (в соответствии с используемым ограничениями) требуемая запоминаемость рекламы, но не удовлетворяется потребность в эмоциональности её восприятия. С другой стороны два ограничивающих условия сами по себе также дают решение: из системы уравнений X Если мы покупаем 2 рекламных блока или 2 площади в газете по 1и 0,5 блока в газете 2, удовлетворяется потребность в запоминаемости и эмоциональности рекламы, причем, стоимость рекламы будет минимальная, а именно 22,5 у.е.В решении этой задачи потребность в запоминаемости и эмоциональности рекламы удовлетворяются полностью. Двойственна рассмотренной задаче задача на нахождение максимума целевой функции. Пусть из рекламных блоков газеты 1и2 необходимо составить характеристику запоминаемости и эмоциональности рекламы: Y Оценка полезности рекламного блока в газете 1 не может превышать 6 у.е., т.е. Y Y=3Y
Связь между двумя задачами проста и легко распространяется на задачи линейного программирования. Обе двойственные задачи имеют одно и то же решение – в том смысле, что функции Z в первой задаче равен максимуму функции Y во второй задаче. Решение задачи (1) следующее: X Далее рассмотрим игру с двумя участниками, платежная матрица которой –квадратная пятого порядка, построенная по данным задач 1 и 2.Где один участник-рекламодатель с желанием минимизации рекламных затрат, другой- рекламное агентство с желанием получить от рекламодателя как можно больший заказ на рекламу. Такая платежная матрица имеет вид: A Нули объясняются тем, что игра справедлива(цена игры равна нулю). Поскольку матрица кососимметрична, оптимальной для обоих игроков является одна и та же смешанная стратегия Z=(Z1,Z2,Z3,Z4,Z5) Оптимальные стратегии Sm=(Z1,Z2,Z3,Z4,Z5) игры с платежной матрицей - A
a -a -a p Решение системы уравнений при данных из таблицы исходных значений параметров дает решение Z1=2, Z2=1\2,Z3=3\2,Z4=9\2 Значит, в решении системы должно соблюдаться соотношение стратегий: Sm=(Z1:Z2:Z3:Z4:Z5)=(2:1\2:3\2:9\2:1) Смысл значения Sm в следующем: для получения требуемой отдачи от рекламных вложений в газетах на единицу стратегии Z5 приходится две единицы стратегии Z1 (например, удвоенная публикация по площади в газете 1); 1\2 единицы Z2 (например, половина площади в газете 2);1,5 единицы Z3 (например, публикация в газете 1 только до уровня информационной насыщенности); 2,5 единицы Z4 (например, публикация в газете 2 до уровня только эмоциональной насыщенности) Соотношение стратегий для решения стоящей проблемы через рекламные ассигнования должны быть в следующих объемах: Q1=200 ед., Q2=50 ед., Q3=150 ед., Q4=450 ед., Q5=100ед. Чтобы получить абсолютные значения Z, необходимо принять во внимание, что для абсолютных значений должно выполняться условие Z1+Z2=Z3+Z4=Z5=1 Нетрудно установить, что мы получили абсолютные величины Z, умножая на 2\19 элементы приведенного соотношения для оптимальных стратегий Sm. Следовательно, решением игры явится смешанная стратегия Sm=(4\19, 1\19,3\19,9\19,2\19), со всеми ранее выявленными соотношениями по рекламному ассигнованию и выбору места. Таким образом, рассмотренная задача представляет собой стратегии рекламодателя –рекламного агентства (игра) или советы как поступиться с рекламным бюджетом предприятия для реализации (выигрыша) поставленной цели.
|

 -реклама в газете1 и X
-реклама в газете1 и X  –реклама в газете 2. Рекламные газеты и рекламные блоки характеризуются двумя показателями – запоминаемости и эмоциональности. Известны следующие данные: один рекламный блок в газете 1 соответствует фактору запоминаемости в1 балл и 1 балл эмоциональности по 5-ти бальной шкале. Реклама в газете 2 соответствует 2 баллам запоминаемости и 4 баллам эмоциональности. По рыночным ценам один блок рекламы в газете 1 стоит 6 у.е., цена в газете 2 стоит 21 у.е. Эти данные можно записать в виде таблицы:
–реклама в газете 2. Рекламные газеты и рекламные блоки характеризуются двумя показателями – запоминаемости и эмоциональности. Известны следующие данные: один рекламный блок в газете 1 соответствует фактору запоминаемости в1 балл и 1 балл эмоциональности по 5-ти бальной шкале. Реклама в газете 2 соответствует 2 баллам запоминаемости и 4 баллам эмоциональности. По рыночным ценам один блок рекламы в газете 1 стоит 6 у.е., цена в газете 2 стоит 21 у.е. Эти данные можно записать в виде таблицы: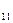 =1
=1
 =2
=2
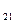 =1
=1
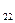 =4
=4
 и при ограничениях:
и при ограничениях:
 , а значит X
, а значит X  . Следовательно, минимальный рекламный бюджет рекламодателя составит 18 у.е., если покупать 3 блока рекламы в газете 1 или устроенную площадь или рекламное место в газете в 3 раза выгоднее, а в газету 2 рекламу вовсе не подавать.
. Следовательно, минимальный рекламный бюджет рекламодателя составит 18 у.е., если покупать 3 блока рекламы в газете 1 или устроенную площадь или рекламное место в газете в 3 раза выгоднее, а в газету 2 рекламу вовсе не подавать. При этом решении удовлетворяются оба требования (в отношении запоминаемости и эмоциональности), но совершенно не принимается во внимание стоимость рекламы.
При этом решении удовлетворяются оба требования (в отношении запоминаемости и эмоциональности), но совершенно не принимается во внимание стоимость рекламы. Аналогично для газеты 2 оценка воздействия рекламы равна Следовательно, двойственную задачу можно сформулировать таким образом: найти такие значения рекламного воздействия газетной рекламы, чтобы
Аналогично для газеты 2 оценка воздействия рекламы равна Следовательно, двойственную задачу можно сформулировать таким образом: найти такие значения рекламного воздействия газетной рекламы, чтобы при условии
при условии
 (минимальная стоимость рекламы в газете).Решение задачи (2): Y
(минимальная стоимость рекламы в газете).Решение задачи (2): Y  (максимальная оценка рекламного бюджета в газетах)
(максимальная оценка рекламного бюджета в газетах)
 могут быть найдены путем решения симметричной пары двойственных задач линейного программирования. Тогда с учетом стратегий по подаче рекламы в газеты, система уравнений по матрице A
могут быть найдены путем решения симметричной пары двойственных задач линейного программирования. Тогда с учетом стратегий по подаче рекламы в газеты, система уравнений по матрице A 

 + b
+ b 
 +b
+b 
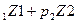 -b
-b 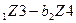 ≤ 0
≤ 0


