Неделя 3
СРСП 5 Тема: Проверка статистических гипотез Цель:Проверить уровень знаний студентов в умении применять основные законы распределения при проверке статистических гипотез Форма проведения:решение задач Задание № 1. Решите следующие задачи: №1 Игральный кубик бросили 60 раз, при этом числа 1, 2, 3, 4, 5, 6 выпали соответственно 12, 9, 13, 11, 8, 7 раз. Можно ли на 5% уровне значимости отвергнуть гипотезу о симметричности кубика? №2 Трое рабочих работают на трех одинаковых станках. В конце смены первый рабочий изготовил 60 деталей, второй – 80, третий – 100 деталей. Можно ли на уровне значимости №3 Станок, работающий со стандартным отклонением №4 Производитель утверждает, что средний вес плитки шоколада не меньше а=50 гр. Инспектор отобрал 10 плиток шоколада и взвесил. Их вес оказался 49, 50, 51, 52, 48, 47, 49, 52 48, 51г соответственно. Не противоречит ли это утверждение производителя? Предполагается, что вес плитки шоколада распределен нормально. Доверительная вероятность р=95%. Задание №2. Выполните тест: 1. Дайте определение статистической гипотезы. a) предположение о том, что случайная величина подчиняется определенному закону распределения, называется статистической гипотезой; b) предположение о том, что случайная величина подчиняется закону распределения Фишера (F-критерий), называется статистической гипотезой; c) предположение о том, что случайная величина подчиняется закону распределения Стьюдента (t-тест), называется статистической гипотезой; d) предположение о том, что случайная величина подчиняется закону распределения Гаусса, называется статистической гипотезой e) предположение о том, что случайная величина подчиняется биномиальному закону распределения, называется статистической гипотезой 2. Что называется проверкой гипотезы? a) процедура сопоставления случайных величин называется проверкой гипотезы; b) проверка гипотезы - это процедура сопоставления высказанной гипотезы с выборочными данными; c) процесс сравнения истинной гипотезы со значениями случайных величин называется проверкой гипотезы; d) процесс сопоставления нуль-гипотезы с теоретическими значениями результативного признака называется проверкой гипотезы e) процесс сравнения истинной гипотезы с результативными значениями случайных величин называется проверкой гипотезы; 3. Какая оценка называется статистической? a) статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин; b) статистической оценкой неизвестного параметра теоретического распределения называют оценку, у которой математическое ожидание равно нулю; c) статистической оценкой неизвестного параметра теоретического распределения называют оценку, которая имеет наименьшую дисперсию; d) статистической оценкой неизвестного параметра теоретического распределения называют оценку, которая стремится по вероятности к оцениваемому параметру; e) статистической оценкой неизвестного параметра теоретического распределения называют оценку, которая имеет наименьшее математическое ожидание. 4. Что называется уровнем значимости при проверке статистических гипотез? a) вероятность попадания случайной величиной в область b) вероятность попадания случайной величиной в область c) значение, определяемое при сравнении нуль - гипотезы и истинной гипотезы d) вероятность попадания случайной величины в критическую область e) значение определяемое при сравнении выдвинутой гипотезы с табличными значениями 5. Какой интервал называется доверительным? a) интервал, который позволяет установить точность оценки; b) интервал, который позволяет установить надежность оценки; c) интервал d) интервал, который удовлетворяет неравенству e) интервал, вероятность которого равна надежности оценки 6. Каким образом записывается
7. Какие ошибки могут возникнуть при проверке статистических гипотез? a) Ошибки спецификации модели. b) Систематические ошибки. c) Ошибки измерений. d) Ошибка первого рода, ошибка второго рода. e) Ошибки выборки. 8. В чем состоит ошибка первого рода при проверке статистических гипотез? a) В том, что будет отвергнута правильная нулевая гипотеза. b) В том, что будет принята нулевая гипотеза, в то время как в действительности верна альтернативная гипотеза. c) В том, что альтернативная гипотеза будет исправлена. d) В том, что правильная гипотеза будет исправлена. Методические рекомендации: Выполнить задания в соответствии с условием (задание № 1). Ответить на тестовые задания в конце занятия для закрепления материала. Литература: 1."Эконометрика" под редакцией И.И. Елисеевой, М: Финансы и статистика", 2002 2."Практикум по эконометрике" под редакцией И.И. Елисеевой, М: Финансы и статистика, 2002 3.Кристофер Доугерти "Введение в эконометрику" М: Ифра-М, 1999 4.Бережная Е.В., Бережной В.И. "Математические методы моделирования экономических систем" М: Финансы и статистика, 2003 5. Ежеманская С.Н. «Эконометрика», Ростов-на-Дону «Феникс», 2003г 6. Кремер Н.Ш., Бутко Б.А. «Эконометрика» М.: ЮНИТИ-ДАНА, 2002г. СРСП 6 Тема: Проверка статистических гипотез Цель:проверить уровень знаний студентов в умении рассчитывать числовые характеристики случайных величин, строить функцию распределения и применять основные законы распределения случайных величин. Форма проведения:индивидуальная лабораторная работа №1 Решите следующие задачи: Вариант № 1 Задача 1.Дан ряд распределения случайной величины Х:
Необходимо: 1) найти математическое ожидание, дисперсию, среднее квадратическое отклонение и коэффициент вариации; 2) определить функцию распределения F(x) и построить ее график; 3) найти вероятность попадания случайно величины в интервал [0,6). Задача 2. Объем продаж товара в течение месяца есть случайная величина, подчиненная нормальному закону распределения с параметрами Вариант № 2 Задача 1. Дан ряд распределения случайной величины Х:
Необходимо: 1) найти математическое ожидание, дисперсию, среднее квадратическое отклонение и коэффициент вариации; 2) определить функцию распределения F(x) и построить ее график; 3) найти вероятность попадания случайной величины в интервал [1,6). Задача 2. Предприятие имеет 5 станков по производству камня работающих независимо дуг от друга. Вероятность отказа любого из них р=0,25. Определите параметры закона биномиального распределения случайной величины число отказов станков. Вариант № 3 Задача 1. Дан ряд распределения случайной величины Х:
Необходимо: 1) найти математическое ожидание, дисперсию, среднее квадратическое отклонение и коэффициент вариации; 2) определить функцию распределения F(x) и построить ее график; 3) найти вероятность попадания случайной величины в интервал [0,5). Задача 2. Производительность труда рабочих некоторого цеха является нормально распределенной случайной величиной с математическим ожиданием 90 кг за смену и стандартным отклонением 15 кг за смену. Вычислите долю рабочих, производительность которых лежит в промежутке от 80 до 110 кг. Вариант № 4 Задача 1. Дан ряд распределения случайной величины Х:
Необходимо: 1) найти математическое ожидание, дисперсию, среднее квадратическое отклонение и коэффициент вариации; 2) определить функцию распределения F(x) и построить ее график; 3) найти вероятность попадания случайной величины в интервал [3,6). Задача 2. Объем продаж товара в течение месяца есть случайная величина, подчиненная нормальному закону распределения с параметрами Методические рекомендации: Индивидуальная лабораторная работа выполняется в отдельных тетрадях. Выполненная работа должна содержать условия задач, формулы, соответствующие расчеты. График функции распределения должен быть выполнен аккуратно, с помощью линейки, в увеличенном масштабе, иметь соответствующие надписи. Литература: 1."Эконометрика" под редакцией И.И. Елисеевой, М: Финансы и статистика", 2002 2."Практикум по эконометрике" под редакцией И.И. Елисеевой, М: Финансы и статистика, 2002 3.Кристофер Доугерти "Введение в эконометрику" М: Ифра-М, 1999 4.Мардас А.Н. "Эконометрика" Учебное пособие, С-Пб "Питер", 2001 5. Ежеманская С.Н. «Эконометрика», Ростов-на-Дону «Феникс», 2003г 6. Кремер Н.Ш., Бутко Б.А. «Эконометрика» М.: ЮНИТИ-ДАНА, 2002г.
|

 принять гипотезу о том, что производительности труда первых двух рабочих равны между собой и в 2 раза меньше производительности третьего рабочего?
принять гипотезу о том, что производительности труда первых двух рабочих равны между собой и в 2 раза меньше производительности третьего рабочего? мм, производит детали средней длины а=20 мм. В случайной выборке объема п=16 деталей средняя длина
мм, производит детали средней длины а=20 мм. В случайной выборке объема п=16 деталей средняя длина  мм. Правильно ли настроен станок? Доверительная вероятность р=99%.
мм. Правильно ли настроен станок? Доверительная вероятность р=99%. , соответствующую нуль - гипотезе;
, соответствующую нуль - гипотезе; , соответствующую истинной гипотезе;
, соответствующую истинной гипотезе; , который покрывает неизвестный параметр с заданной надежностью
, который покрывает неизвестный параметр с заданной надежностью  ;
; ;
; -распределение?
-распределение?

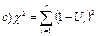


 =500 и
=500 и  =120 д.ед. Определите вероятность продажи товара в течение одного месяца на сумму от 480 до 600 д.ед.
=120 д.ед. Определите вероятность продажи товара в течение одного месяца на сумму от 480 до 600 д.ед.


