Неделя 2
СРСП 3 Тема: Сведения из теории вероятностей и математической статистики Цель:Проверить уровень знаний студентов в умении применять основные законы распределения случайных величин. Форма проведения:решение задач Задание № 1.Решите следующие задачи: №1 Автобусы пребывают на остановку через 5 минут. Какова вероятность того, что время ожидания автобуса не превысит 4 минуты? №2 Техническая система состоит из пяти независимо друг от друга функционирующих узлов. Определить математическое ожидание, дисперсию, среднее квадратическое отклонение числа отказа узлов, если вероятность отказа любого из них равна 0,2 (биномиальное распределение). №3 На базу отправлено 10000 изделий. Вероятность того, что изделие в пути получит повреждение, равна 0,0003. Найти вероятность того, что на базу прибудут 4 поврежденных изделия. №4 Объем продаж товара в течение месяца есть случайная величина, подчиненная нормальному закону распределения с параметрами Задание №2. Выполните тест: 1. Какими параметрами характеризуется биномиальное распределение случайных величин? a) Количеством испытаний п и вероятностью наступления события А – р b) Математическим ожиданием М(Х) и дисперсией D(Х) c) Параметром l и вероятностью наступления события А – р d) Вероятностью наступления события А – р и вероятностью ненаступления события А – q e) Среднеквадратическим отклонением 2. Каким параметром характеризуется закон распределения Пуассона? a) случайной величиной у; b) дисперсией D(X); c) средним значением М(Х); d) среднеквадратическим отклонением e) случайной величиной х. 3. Какими параметрами характеризуется закон распределения Фишера? a) числом степеней свободы b) числами степеней свободы c) генеральными дисперсиями d) дисперсией e) числом наблюдений п. 4. Какие необходимо знать параметры, чтобы задать нормальное распределение случайной величины?
5. Как записывается показательное распределение случайной величины Х? a) b) c) d) e) Методические рекомендации: Выполнить задания в соответствии с условием (задание № 1). Ответить на тестовые задания в конце занятия для закрепления материала. Литература: 1."Эконометрика" под редакцией И.И. Елисеевой, М: Финансы и статистика", 2002 2."Практикум по эконометрике" под редакцией И.И. Елисеевой, М: Финансы и статистика, 2002 3.Кристофер Доугерти "Введение в эконометрику" М: Ифра-М, 1999 4.Бережная Е.В., Бережной В.И. "Математические методы моделирования экономических систем" М: Финансы и статистика, 2003 СРСП 4 Тема: Сведения из теории вероятностей и математической статистики Цель:Проверить уровень знаний студентов в умении строить доверительные интервалы. Форма проведения:решение задач Задание № 1. Решите следующие задачи: №1 Производительность труда рабочих некоторого цеха является нормально распределенной случайной величиной с математическим ожиданием 90 кг за смену и стандартным отклонением 15 кг за смену. Вычислите долю рабочих, производительность которых: 1) лежит в промежутке от 80 до 110 кг за смену; 2) превышает 110 кг за смену; 3) не менее 80 кг; 4) какой следует установить норму дневной выработки, чтобы 90% рабочих её выполнили. №2 Произведена выборка объема п=1000 штук. 120 из них оказались бракованными. Найти доверительный интервал доли бракованных изделий в генеральной совокупности для доверительной вероятности р=99% №3 Выборка из большой партии электроламп содержит 100 ламп. Средняя продолжительность работы лампы из выборки оказалась равной 1000 ч. Найти 95% доверительный интервал для средней продолжительности работы лампы, случайно выбранной из всей партии, если время работы является нормально распределенной случайной величиной со стандартным отклонением 40 ч. Задание №2. Выполните тест: 1. Какие виды оценок существуют? a) Эффективные и неэффективные b) Точечные и интервальные c) Несмещенные и смещенные d) Состоятельные и несостоятельные e) Доверительные и вероятностные 2. Какими свойствами должна обладать статистическая оценка? a) Статистическая оценка должна быть смещенной и точной. b) Статистическая оценка должна быть несмещенной, эффективной и состоятельной. c) Статистическая оценка должна иметь наименьшую дисперсию. d) Статистическая оценка не должна иметь систематической ошибки и иметь наименьшую дисперсию. e) Статистическая оценка должна быть смещенной и не иметь систематической ошибки. 3. Какая статистическая оценка называется несмещенной? a) Если она имеет наименьшую дисперсию: b) Если её математическое ожидание равно оцениваемому параметру: c) Оценка, которая дает точное значение для большой выборки: d) Если она имеет наименьшее математическое ожидание: e) Если ее дисперсия равна оцениваемому параметру: 4. Какая оценка называется интервальной? a) Числовое значение параметра b) Функция результатов наблюдения над случайной величиной Х, с помощью которой судят о значениях параметра c) Интервал d) Интервал, в котором находится оцениваемый параметр 5. Какая оценка называется точечной? a) Числовое значение параметра b) Интервал c) Функция результатов наблюдения над случайной величиной Х, с помощью которой судят о значениях параметра d) Интервал, в котором находится оцениваемый параметр Методические рекомендации: Выполнить задания в соответствии с условием (задание № 1). Ответить на тестовые задания в конце занятия для закрепления материала. Литература: 1."Эконометрика" под редакцией И.И. Елисеевой, М: Финансы и статистика", 2002 2."Практикум по эконометрике" под редакцией И.И. Елисеевой, М: Финансы и статистика, 2002 3.Кристофер Доугерти "Введение в эконометрику" М: Ифра-М, 1999 4.Мардас А.Н. "Эконометрика" Учебное пособие, С-Пб "Питер", 2001 5.Бережная Е.В., Бережной В.И. "Математические методы моделирования экономических систем" М: Финансы и статистика, 2003
|

 =500 и
=500 и  д.ед. Определите вероятность продажи товара в течение одного месяца на сумму от 480до 600 д.ед.
д.ед. Определите вероятность продажи товара в течение одного месяца на сумму от 480до 600 д.ед. и математическим ожиданием М(Х)
и математическим ожиданием М(Х) ;
;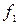 ;
; ;
; и
и  ;
; и среднеквадратическим отклонением
и среднеквадратическим отклонением  ;
;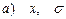

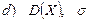
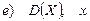
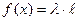



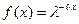

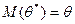


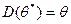
 , полученное по выборке объема п.
, полученное по выборке объема п. внутри, которого с наперед заданной вероятностью
внутри, которого с наперед заданной вероятностью  находится точное значение оцениваемого параметра
находится точное значение оцениваемого параметра 


