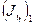ГОУ ВПО. Лабораторная работа На тему: “Изучение законов сохранения в механике”
Лабораторная работа
21040165 03М 911 Шифр Номер работы Группа
Черных Д. С. Проверил: Бодров Е. А.
Цель работы: Изучить законы сохранения в механике и измерить коэффициент восстановления при ударе шаров. Приборы и оборудование: Установка для изучения упругого и неупругого удара шаров, шары, линейка. Краткая теория: Для характеристики механического состояния при движении тела вводится физическая величина – импульс. Импульс – это векторная величина, численно равная произведению массы тела на его скорость и имеющая направление, совпадающее с направлением скорости тела. Согласно второго закона динамики: скорость изменения импульса тела равна по величине действующей силе и совпадает с ней по направлению. Т.о., любое изменение импульса этого тела может происходить только при действии сил. Рассматривая систему тел, ее импульс определяется как векторная сумма импульсов тел, входящих в систему. Силы взаимодействия между телами, входящими в рассматриваемую систему, называются внутренними. Силы, действующие на систему со стороны других тел, не входящих в рассматриваемую систему, называются внешними. Механические системы, на которые внешние силы не действуют, называются изолированными или замкнутыми. В замкнутой системе тел суммарный импульс системы остается постоянным – в этом заключается закон сохранения импульса. Введение понятия импульса, как меры механического движения не всегда пригодно для оценки изменения движения тела. Более универсальной мерой движения является энергия. Энергия – скалярная физическая величина, являющаяся общей мерой различных форм движения материи, рассматриваемых в физике. Энергия бывает механической, внутренней, электромагнитной, ядерной и т.д. Энергия является важнейшей физической величиной, характеризующей способность тел или системы тел совершать работу, и измеряется величиной работы, которую при определенных условиях может совершить система. Существует две разновидности механической энергии: кинетическая (обусловлена движением тел и зависит от скорости движения) и потенциальная (обусловлена взаимным расположением всех частей системы во внешнем поле потенциальных сил). Сумма кинетической и потенциальной энергии называется полной механической энергией. Для замкнутой системы тел, в которой действуют только консервативные силы, полная механическая энергия системы остается постоянной – в этом заключается закон сохранения механической энергии. Использование законов сохранения энергии и импульса позволяет решать многие задачи механики, не прибегая непосредственно к уравнениям движения. Превращения кинетической энергии в потенциальную и обратно наблюдаются при ударе тел. Удар – кратковременное взаимодействие тел, при этом оба тела деформируются и возникают ударные силы значительной величины. Различают два предельных случая: абсолютно упругий и абсолютно неупругий удары. При абсолютно упругом ударе на фазе сближения тел кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации, на фазе разлета тела снова приобретают первоначальную форму, отталкивая друг друга. В итоге потенциальная энергия упругой деформации опять переходит в кинетическую и тела разлетаются. При абсолютно упругом ударе механическая энергия тел не переходит в другие немеханические виды энергии. Отметим также, что при абсолютно упругом ударе не выделяется теплота, следовательно, систему из двух взаимодействующих шаров можно считать замкнутой. К такой системе можно применить закон сохранения энергии и импульса. Абсолютно упругий удар является идеальным случаем. В реальных случаях в зависимости от того, из какого вещества изготовлены шары, большая или меньшая часть механической энергии переходит в тепло. Абсолютно неупругий удар характеризуется тем, что потенциальная энергия упругой деформации не возникает, кинетическая энергия тел полностью или частично превращается во внутреннею энергию, после удара сталкивающиеся тела либо покоятся, либо движутся с одинаковой скоростью. Классическая теория удара предполагает, что все элементы каждого тела жестко связаны и будут мгновенно испытывать одинаковое изменение движения, являющееся результатом удара. В действительности возмущение, порожденное в точке соударения, распространяется в телах с конечной скоростью, и его отражение от граничных поверхностей вызывает колебания и вибрации в телах. Местные быстроизменяющиеся деформации и механические напряжения, вызванные этим возмущением, не могут быть определены методами классической теории, но могут быть исследованы с помощью рассмотрения волнового явления. Следует отметить, что при решении задач с использованием волновой теории удара возникают большие погрешности и неточности, связанные с математической сложностью вывода формул и расчетов.
Расчетные формулы:
Замечание: Значения средних углов отклонения второго шара до удара, первого шара после удара, второго шара после удара, средних значений скоростей шаров до и после удара, средних значений импульсов шаров до и после удара рассчитываются по аналогичной формуле (
Замечание: Значения скоростей правого шара до удара, а также левого и правого шаров после удара рассчитываются по данной формуле.
Проведем соответствующие расчеты и измерения:
Систематизируем результаты в виде таблиц:
Вывод: Выполнив данную работу я на практике проверил закон сохранения импульса для удара двух деревянных шаров, близкого к абсолютно упругому. Я употребил фразу “близкого к абсолютно упругому” на следующих основаниях: дерево – материал не склонный к сильным деформациям при ударах с небольшой силой предметов с малыми массами; а кроме того, при подсчетах выяснилось, что значения импульса ударяющего шара до удара и ударяемого шара после удара практически одинаково, иными словами, импульс перешел почти без потерь. Также я рассчитал коэффициент восстановления для данной установки, он оказался равен −0,9218. В качестве измерительных приборов и оборудования мною были использованы: установка для изучения упругого и неупругого удара шаров, шары, линейка.
ГОУ ВПО ДВГУПС
Лабораторная работа
21040165 04М 911 Шифр Номер работы Группа
Черных Д. С. Проверил: Бодров Е. А.
Цель работы: Определить момент инерции цилиндров с помощью маятника Обербека.
Приборы и оборудование: 1. Маятник Обербека 2. Набор грузов 3. Секундомер 4. Масштабная линейка; штангенциркуль 5. Четыре одинаковых по массе, форме и размерам цилиндра Краткая теория: При вращении твердого тела вокруг неподвижной оси его инерциальные свойства определяются не только массой тела, но и распространением этой массы относительно оси вращения. Твердое тело, состоящее из материальных точек, имеющих массу, участвует во вращательном движении. Мерой инерции каждой материальной точки вращающегося твердого тела является момент инерции. Относительно неподвижной оси он равен произведению массы этой точки на квадрат расстояния от точки до оси вращения. Для тела любой геометрической формы момент инерции относительно неподвижной оси равен сумме моментов инерции всех его точек относительно этой оси. Что касается тел правильной геометрической формы – для них выведены специальные формулы расчета моментов инерции. При изменении положения оси вращения относительно центра масс изменяется и момент инерции тела. При параллельном переносе оси вращения справедлива теорема Штейнера. По ней определяют момент инерции твердого тела любой геометрической формы относительно нецентральной оси. Теорема Штейнера: если ось вращения, проходящую через центр массы тела, переместить параллельно самой себе на расстояние Основной закон динамики вращательного движения можно получить из второго закона Ньютона для поступательного движения твердого тела. На основании того, что если к твердому телу массой Представив В замкнутой системе вращающихся тел выполняется закон сохранения момента импульса: изменение момента импульса вращающихся тел в замкнутой системе равен нулю. Поступательно движущиеся тела обладают кинетической энергией. Движение вращающегося тела характеризуется угловой скоростью, а мерой его инертности является момент инерции. Исходя из связи линейной и угловой скоростей, и проведя математические преобразования стандартной формулы кинетической энергии, получим За промежуток времени вращающееся тело совершит работу, равную произведению момента силы на угол поворота, сделанный радиусом этого тела. Т.е. Работу, совершенную вращающимся телом за единицу времени называют мощностью вращающегося тела. Она равна
Расчетные формулы:
Проведем соответствующие расчеты и измерения:
Систематизируем результаты в виде таблиц: Примечание: Все значения в таблице приведены в соответствии с системой СИ.
Вывод: Выполнив данную работу, определил момент инерции цилиндров с помощью маятника Обербека, ознакомился с тонкостями законов динамики вращательного движения твердого тела и законов сохранения момента импульса, а также проверил на опыте теорему Штейнера. В ходе работы мною были проведены прямые измерения некоторых параметров лабораторной установки – таких, как радиус шкива маятника, высота подъема груза над полом, масса грузов, диаметры цилиндров, время падения грузов и т.д. Далее, на основании полученных прямых измерений я провел косвенные измерения среднего времени падения грузов, среднего ускорения падения грузов для каждого опыта в отдельности, и, собственно, момента инерции для каждого опыта в отдельности и его среднее значение для пар опытов. Значения моментов инерции цилиндров относительно центральной оси я находил по двум формулам: по формуле, выведенной из второго закона Ньютона и по теореме Штейнера. После сравнения полученных результатов оказалось, что значения вычисленных величин разнятся пренебрежимо мало и то в силу погрешностей при измерениях. В качестве измерительных приборов и лабораторного оборудования мною были использованы: маятник Обербека, набор грузов, секундомер, масштабная линейка, штангенциркуль, отвертка, четыре одинаковых по массе, форме и размерам цилиндра.
|
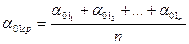- расчет среднего значение угла отклонения левого шара до удара.
).
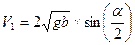- скорость левого шара до удара.
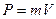- импульс тела
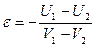- коэффициент восстановления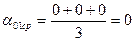
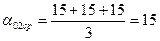
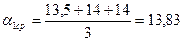
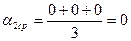
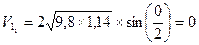
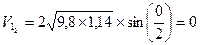
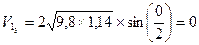
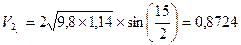
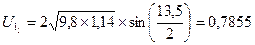
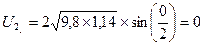
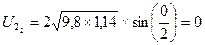
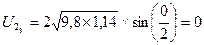
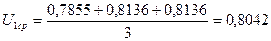
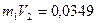
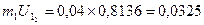
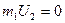
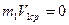
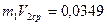
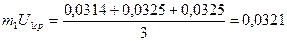
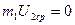
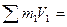0 
0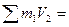,8724+0,8724+0,8724=0,1047 
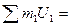0,0314+0,0325+0,0325=0,0964 
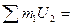0 
,
,
,
,
,
,
,
,
,
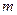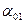
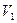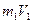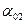
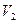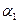
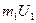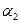
, то момент инерции относительной этой оси будет равен алгебраической сумме момента инерции тела 
, относительно центральной оси вращения, и произведению массы тела 
на квадрат расстояния 
.
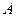приложить некоторую силу 
, то в результате жесткой связи между всеми материальными точками тела все они получат угловое ускорение 
и соответственные линейные ускорения, как если бы на каждую точку действовала определенная сила. Далее производятся некоторые математические преобразования следствием которых является формула момента силы 
- основной закон динамики вращательного движения твердого тела. Закон формулируется так: момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение.
по времени 
, подставляем это в формулу основного закона. Отсюда можно получить еще одну формулировку этого закона: импульс момента силы, действующий на вращательное тело, равен изменению его момента импульса.
.
.
- среднее значение времени падения груза
- среднее значение ускорения груза при падении
- момент инерции (для каждого опыта в отдельности)
- среднее значение моментов инерции (для первой и второй пары опытов в отдельности)
- момент инерции цилиндра относительно центральной оси (теорема Штейнера)
- момент инерции цилиндра относительно центральной оси
- среднее время падения груза массой 200 грамм
- среднее время падения груза массой 300 грамм
- среднее время падения груза массой 300 грамм с цилиндрами, установленными на спицах маятника на расстоянии r1
- среднее время падения груза массой 300 грамм с цилиндрами, установленными на спицах маятника на расстоянии r2
- ускорение падения груза массой 200 грамм
- ускорение падения груза массой 300 грамм
- ускорение падения груза массой 300 грамм с цилиндрами, установленными на спицах маятника на расстоянии r1
- ускорение падения груза массой 300 грамм с цилиндрами, установленными на спицах маятника на расстоянии r2
- момент инерции для первого опыта
- момент инерции для второго опыта
- момент инерции для третьего опыта
- момент инерции для четвертого опыта
- среднее значение момента инерции для первой пары опытов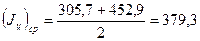
- среднее значение момента инерции для второй пары опытов
305,699
452,898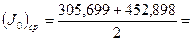
379,299 - момент инерции цилиндра относительно центральной оси (теорема Штейнера)
379,296 - момент инерции цилиндра относительно центральной оси
0,1965
0,2
0,3
0,3
0,131
0,165
