Уравнение стоячей волны.Напишем уравнения двух плоских волн, распространяющихся вдоль оси х в противоположных направлениях:
Преобразовав это уравнение, получим упрощенное уравнение стоячей волны: 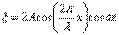В каждой точке этой волны происходят колебания той же частоты w с амплитудой Aст=|2А*cos(2pх/l)|, зависящей от координаты х рассматриваемой точки. В точках среды, где Для образования стоячей волны в ограниченной среде нужно, как мы говорили, чтобы бегущая и отраженная волны усиливали друг друга, в частности, в точке 0, где расположен источник. Тогда в момент времени t фаза источника в отраженной волне должна быть (at 2пк, и произвольное число слагаемых 2я под знаком косинуса можно опустить.
|
Сложив вместе эти уравнения и преобразовав результат по формуле для суммы косинусов, получим уравнение стоячей волны:
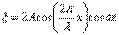
амплитуда колебаний достигает максимального значения, равного 2А. В точках среды, где 
амплитуда колебаний обращается в нуль. Точки, в которых амплитуда колебаний максимальна (Аст=2А), называются пучностями стоячей волны, а точки, в которых амплитуда колебаний равна нулю (Aст=0), называются узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. В случае же стоячей волны переноса энергии нет, так как падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях. Поэтому полная энергия результирующей стоячей волны, заключенной между узловыми точками, остается постоянной. Лишь в пределах расстояний, равных половине длины волны, происходят взаимные превращения кинетической энергии в потенциальную и обратно.
