Тангенциальная составляющая ускорения 8 страница
7.1. Определить собственную длину стержня (длину, измеренную в системе, относительно которой стержень покоится), если в лабораторной системе (системе отсчета, связанной с измерительными приборами) его скорость v = 0,8 с, длина l = 1 м и угол между ним и направлением движения q = 30°.
7.2. Собственное время жизни частицы отличается на 1,5% от времени жизни по неподвижным часам. Определить b = v / с. [0,172] 7.3. Тело, масса покоя которого 2 кг, движется со скоростью 200 Мм/с в системе K', перемещающейся относительно системы К со скоростью 200 Мм/с. Определить: 1) скорость тела относительно системы К; 2) его массу в этой системе. [1) 277 Мм/с; 2) 5,2 кг] 7.4. Воспользовавшись тем, что интервал — инвариантная величина по отношению к преобразованиям координат, определить расстояние, которое пролетел p-мезон с момента рождения до распада, если время его жизни в этой системе отсчета D t = 5 мкс, а собственное время жизни (время, отсчитанное по часам, движущимся вместе с телом) D t 0 =2,2 мкс. [1,35 км] 7.5. Определить скорость, при которой релятивистский импульс частицы превышает ее ньютоновский импульс в пять раз. [0,98 с] 7.6. Определить скорость, полученную электроном, если он прошел ускоряющую разность потенциалов 1,2 МэВ. [2,86 Мм/с] 7.7. Определить релятивистский импульс электрона, кинетическая энергия которого 1 ГэВ. [5,34×10–19 Н×с] 2 ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ Глава 8 Молекулярно-кинетическая теория идеальных газов § 41. Статистический и термодинамический методы. Опытные законы идеального газа Статистический и термодинамический методы исследования. Молекулярная физика и термодинамика — разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно дополняющих друг друга метода: статистический (молекулярно-кинетический) и термодинамический. Первый лежит в основе молекулярной физики, второй — термодинамики. Молекулярная физика — раздел физики, изучающий строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении. Идея об атомном строении вещества высказана древнегреческим философом Демокритом (460—370 до н. э.). Атомистика возрождается вновь лишь в XVII в. и развивается в работах М. В. Ломоносова, взгляды которого на строение вещества и тепловые явления были близки к современным. Строгое развитие молекулярной теории относится к середине XIX в. и связано с работами немецкого физика Р. Клаузиуса (1822—1888), Дж. Максвелла и Л. Больцмана. Процессы, изучаемые молекулярной физикой, являются результатом совокупного действия огромного числа молекул. Законы поведения огромного числа молекул, являясь статистическими закономерностями, изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы в конечном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц (скорости, энергии и т. д.). Например, температура тела определяется скоростью хаотического движения его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорости движения молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики тел имеют физический смысл лишь в случае большого числа молекул. Термодинамика — раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями. Термодинамика не рассматривает микропроцессы, которые лежат в основе этих превращений. Этим термодинамический метод отличается от статистического. Термодинамика базируется на двух началах — фундаментальных законах, установленных в результате обобщения опытных данных. Область применения термодинамики значительно шире, чем молекулярно-кинетической теории, ибо нет таких областей физики и химии, в которых нельзя было бы пользоваться термодинамическим методом. Однако, с другой стороны, термодинамический метод несколько ограничен: термодинамика ничего не говорит о микроскопическом строении вещества, о механизме явлений, а лишь устанавливает связи между макроскопическими свойствами вещества. Молекулярно-кинетическая теория и термодинамика взаимно дополняют друг друга, образуя единое целое, но отличаясь различными методами исследования. Термодинамика имеет дело с термодинамической системой — совокупностью макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой). Основа термодинамического метода — определение состояния термодинамической системы. Состояние системы задается термодинамическими параметрами (параметрами состояния) — совокупностью физических величин, характеризующих свойства термодинамической системы. Обычно в качестве параметров состояния выбирают температуру, давление и удельный объем. Температура — одно из основных понятий, играющих важную роль не только в термодинамике, но и в физике в целом. Температура — физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. В соответствии с решением XI Генеральной конференции по мерам и весам (1960) в настоящее время можно применять только две температурные шкалы — термодинамическую и Международную практическую, градуированные соответственно в кельвинах (К) и в градусах Цельсия (°С). В Международной практической шкале температура замерзания и кипения воды при давлении 1,013×105 Па соответственно 0 и 100°С (реперные точки). Термодинамическая температурная шкала определяется по одной реперной точке, в качестве которой взята тройная точка воды (температура, при которой лед, вода и насыщенный пар при давления 609 Па находятся в термодинамическом равновесии). Температура этой точки по термодинамической шкале равна 273,16 К (точно). Градус Цельсия равен кельвину. В термодинамической шкале температура замерзания воды равна 273,15 К (при том же давлении, что и в Международной практической шкале), поэтому, по определению, термодинамическая температура и температура по Международной практической шкале связаны соотношением Т = 273,15 + t. Температура T = 0 К называется нулем кельвин. Анализ различных процессов показывает, что 0 К недостижим, хотя приближение к нему сколь угодно близко возможно. Удельный объем v — это объем единицы массы. Когда тело однородно, т. е. его плотность r = const, то v=V/m= 1 /p. Так как при постоянной массе удельный объем пропорционален общему объему, то макроскопические свойства однородного тела можно характеризовать объемом тела. Параметры состояния системы могут изменяться. Любое изменение в термодинамической системе, связанное с изменением хотя бы одного из ее термодинамических параметров, называется термодинамическим процессом. Макроскопическая система находится в термодинамическом равновесии, если ее состояние с течением времени не меняется (предполагается, что внешние условия рассматриваемой системы при этом не изменяются). В молекулярно-кинетической теории пользуются идеализированной моделью идеального газа, согласно которой считают, что: 1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда; 2) между молекулами газа отсутствуют силы взаимодействия; 3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие. Модель идеального газа можно использовать при изучении реальных газов, так как они в условиях, близких к нормальным (например, кислород и гелий), а также при низких давления» и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки, учитывающие собственный объем молекул газа и действующие молекулярные силы, можно перейти к теории реальных газов. Рассмотрим законы, описывающие поведение идеальных газов. Закон Бойля—Мариотта *: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная:
* Р. Бойль (1627—1691)—английский ученый; Э. Мариотт (1620—1684) — французский физик.
Кривая, изображающая зависимость между величинами р и V, характеризующими свойства вещества при постоянной температуре, называется изотермой. Изотермы представляют собой гиперболы, расположенные на графикетем выше, чем выше температура, при которой происходит процесс (рис. 60). Законы Гей-Люссака *:1) объем данной массы газа при постоянном давлении изменяется линейно с температурой: (41.2) 2) давление данной массы газа при постоянном объеме изменяется линейно с температурой: (41.3) * Ж. Гей-Люссак (1778—1850) — французский ученый.
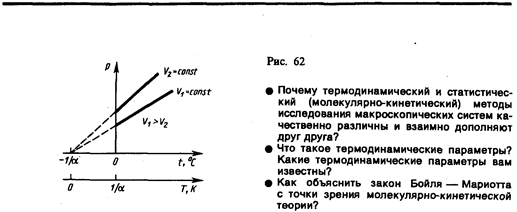
В этих уравнениях t — температура по шкале Цельсия, р 0 и V 0 — давление и объем при 0°С, коэффициент a = 1/273,15 К–1. Процесс, протекающий при постоянном давлении, называется изобарным. На диаграмме в координатах V, t (рис. 61) этот процесс изображается прямой, называемой изобарой. Процесс, протекающий при постоянном объеме, называется изохорным. На диаграмме в координатах р, t (рис. 62) он изображается прямой, называемой изохорой. Из (41.2) и (41.3) следует, что изобары и изохоры пересекают ось температур в точке t=– 1 /a=– 273,15°С, определяемой из условия 1+a t = 0. Если перенести начало отсчета в эту точку, то происходит переход к шкале Кельвина (рис. 62), откуда
Вводя в формулы (41.2) и (41.3) термодинамическую температуру, законам Гей-Люссака можно придать более удобный вид:
(41.4) (41.5) где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной изобаре или изохоре.
Закон Авогадро *: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы. При нормальных условиях этот объем равен 22,41×10–3 м3/моль. * А. Авогадро (1776—1856) — итальянский физики химик.
По определению, в одном моле различных веществ содержится одно и то же число молекул, называемое постоянной Авогадро:
Закон Дальтона *: давление смеси идеальных газов равно сумме парциальных давлений p 1, p 2 ,..., рn входящих в нее газов:
Парциальное давление — давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре. * Дж. Дальтон (1766—1844) — английский химик и физик.
§ 42. Уравнение Клапейрона — Менделеева Как уже указывалось, состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением р, объемом V и температурой Т. Между этими параметрами существует определенная связь, называемая уравнением состояния, которое в общем виде дается выражением
где каждая из переменных является функцией двух других. Французский физик и инженер Б. Клапейрон (1799—1864) вывел уравнение состояния идеального газа, объединив законы Бойля — Мариотта и Гей-Люссака. Пусть некоторая масса газа занимает объем V 1, имеет давление р 1 и находится при температуре T 1. Эта же масса газа в другом произвольном состоянии характеризуется параметрами р 2, V 2, T 2 (рис. 63). Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: 1) изотермического (изотерма 1–1'), 2) изохорного (изохора 1'–2).
В соответствии с законами Бойля — Мариотта (41.1) и Гей-Люссака (41.5) запишем:
Исключив из уравнений (42.1) и (42.2)
Так как состояния 1 и 2 были выбраны произвольно, то для данной массы газа величина pV/T остается постоянной, т. е.
Выражение (42.3) является уравнением Клапейрона, в котором В — газовая постоянная, различная для разных газов. Русский ученый Д. И. Менделеев (1834—1907) объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (42.3) к одному молю, использовав молярный объем V m. Согласно закону Авогадро, при одинаковых р и Т моли всех газов занимают одинаковый молярный объем V m, поэтому постоянная В будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется молярном газовой постоянной. Уравнению
удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона — Менделеева. Числовое значение молярной газовой постоянной определим из формулы (42.4), полагая, что моль газа находится при нормальных условиях (р 0 = 1,013×105 Па, T 0=273,15 К, V m=22,41×10–3 м3/моль): R =8,31 Дж/(моль×К). От уравнения (42.4) для моля газа можно перейти к уравнению Клапейрона — Менделеева для произвольной массы газа. Если при некоторых заданных давлении и температуре один моль газа занимает молярный объем V m, то при тех же условиях масса т газа займет объем V= (т/М)V m, где М — молярная масса (масса одного моля вещества). Единица молярной массы — килограмм на моль (кг/моль). Уравнение Клапейрона — Менделеева для массы т газа
где n =m/M — количество вещества.
Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана:
Исходя из этого уравнение состояния (42.4) запишем в виде
где N A /V m = n — концентрация молекул (число молекул в единице объема). Таким образом, из уравнения
следует, что давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1 м3 газа при нормальных условиях, называется числом Лошмидта *:
* И. Лошмидт (1821—1895) —австрийский химик и физик.
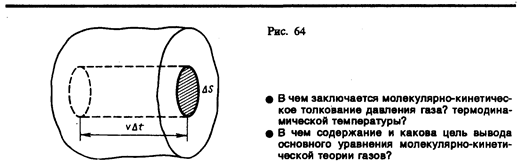
§ 43. Основное уравнение молекулярно-кинетической теории идеальных газов Для вывода основного уравнения молекулярно-кинетической теории рассмотрим одноатомный идеальный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку D S (рис. 64) и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, движущаяся перпендикулярно площадке, передает ей импульс m 0 v – (– m 0 v) = 2 m 0 v, где m 0 — масса молекулы, v — ее скорость. За время D t площадки D S достигнут только те молекулы, которые заключены в объеме цилиндра с основанием D S и высотой v D t (рис. 64). Число этих молекул равно n D Sv D t (n — концентрация молекул). Необходимо, однако, учитывать, что реально молекулы движутся к площадке D S под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул, причем половина молекул 1/6 движется вдоль данного направления в одну сторону, половина — в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку D S будет 1/6 n D Sv D t. При столкновении с площадкой эти молекулы передадут ей импульс
Тогда давление газа, оказываемое им на стенку сосуда,
Если газ в объеме V содержит N молекул, движущихся со скоростями v 1, v 2 ,..., vN, то целесообразно рассматривать среднюю квадратную скорость
характеризующую всю совокупность молекул газа. Уравнение (43.1) с учетом (43.2) примет вид
Выражение (43.3) называется основным уравнением молекулярно-кинетической теории идеальных газов. Точный расчет с учетом движения молекул по всевозможным направлениям дает ту же формулу. Учитывая, что n =N / V, получим
или
где Е — суммарная кинетическая энергия поступательного движения всех молекул газа. Так как масса газа m=Nm 0, то уравнение (43.4) можно переписать в виде
Для одного моля газа т=М (М — молярная масса), поэтому
где V m — молярный объем. С другой стороны, по уравнению Клапейрона — Менделеева, pV m =RT. Таким образом,
откуда
Так как M=m 0 N А, где т 0 — масса одной молекулы, a N А — постоянная Авогадро, то из уравнения (43.6) следует, что
где k=R/N А — постоянная Больцмана. Отсюда найдем, что при комнатной температуре молекулы кислорода имеют среднюю квадратичную скорость 480 м/с, водорода — 1900 м/с. При температуре жидкого гелия те же скорости будут соответственно 40 и 160 м/с. Средняя кинетическая энергия поступательного движения одной молекулы идеального газа
(использовали формулы (43.5) и (43.7)) пропорциональна термодинамической температуре и зависит только от нее. Из этого уравнения следует, что при Т =0 <e0>=0, т. е. при 0К прекращается поступательное движение молекул газа, а следовательно, его давление равно нулю. Таким образом, термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газа, и формула (43.8) раскрывает молекулярно-кинетическое толкование температуры. § 44. Закон Максвелла о распределении молекул идеального газа по скоростям и энергиям теплового движения При выводе основного уравнения молекулярно-кинетической теории молекулам задавали различные скорости. В результате многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Однако из-за хаотического движения молекул все направления движения являются равновероятными, т. е. в любом направлении в среднем движется одинаковое число молекул. По молекулярно-кинетической теории, как бы ни изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул массой т 0 в газе, находящемся в состоянии равновесия при Т = const. остается постоянной и равной Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом. При выводе закона распределения молекул по скоростям Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют. Закон Максвелла описывается некоторой функцией f (v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные d v, то на каждый интервал скорости будет приходиться некоторое число молекул d N(v), имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул d N(v)/N, скорости которых лежат в интервале от v до v+ d v, т. е.
откуда
Применяя методы теории вероятностей. Максвелл нашел функцию f(v) — закон о распределеня молекул идеального газа по скоростям:
Из (44.1) видно, что конкретный вид функции зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т). График функции (44.1) приведен на рис. 65. Так как при возрастании v множитель exp[ –m 0 v2/(2kT) ] уменьшается быстрее, чем растет множитель v 2, то функция f(v), начинаясь от нуля, достигает максимума при v B, и затем асимптотически стремится к нулю. Кривая несимметрична относительно v B. Относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+ d v, находится как площадь заштрихованной полоски на рис. 65. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция f(v) удовлетворяет условию нормировки
Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. Значение наиболее вероятной скорости можно найти продифференцировав выражение (44.1) (постоянные множители опускаем) по аргументу v, приравняв результат нулю и используя условие для максимума выражения f(v):
Значения v= 0 и v =¥ соответствуют минимумам выражения (44.1), а значение v, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость v B:
Из формулы (44.2) следует, что при повышении температуры максимум функции распределения молекул по скоростям (рис. 66) сместится вправо (значение наиболее вероятной скорости становится больше). Однако площадь, ограниченная кривой, остается неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться. Средняя скорость молекулы < v > (средняя арифметическая скорость) определяется по формуле
Подставляя сюда f(v) и интегрируя, получаем
Скорости, характеризующие состояние газа: 1) наиболее вероятная
можно найти распределение молекул газа по значениям кинетической энергии e. Для этого перейдем от переменной v к переменной e =m 0 v 2 / 2. Подставив в (44.4) v=
где d N (e) — число молекул, имеющих кинетическую энергию поступательного движения, заключенную в интервале от e до e + d e. Таким образом, функция распределения молекул по энергиям теплового движения
Средняя кинетическая энергия < e > молекулы идеального газа
т. е. получили результат, совпадающий с формулой (43.8).
§ 45. Барометрическая формула. Распределение Больцмана При выводе основного уравнения молекулярно-кинетической теории газов и максвелловского распределения молекул по скоростям предполагалось, что на молекулы газа внешние силы не действуют, поэтому молекулы равномерно распределены по объему. Однако молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение, с одной стороны, и тепловое движение молекул — с другой, приводят к некоторому стационарному состоянию газа, при котором давление газа с высотой убывает.
|


 (41.1)
(41.1)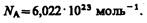
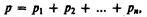
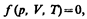
 (42.1)
(42.1) (42.2)
(42.2) получим
получим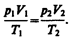
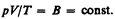 (42.3)
(42.3)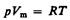 (42.4)
(42.4)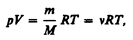 (42.5)
(42.5)

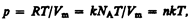
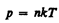 (42.6)
(42.6)

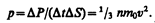 (43.1)
(43.1) (43.2)
(43.2)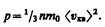 (43.3)
(43.3)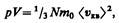 (43.4)
(43.4)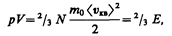 (43.5)
(43.5)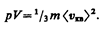
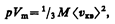

 (43.6)
(43.6) (43.7)
(43.7)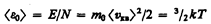 (43.8)
(43.8)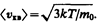
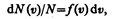
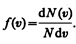
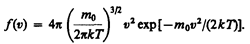 (44.1)
(44.1)

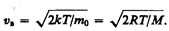 (44.2)
(44.2)
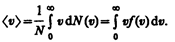
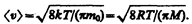 (44.3)
(44.3)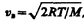 2) средняя
2) средняя 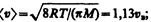 3) средняя квадратичная
3) средняя квадратичная 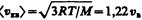 (рис. 65). Исходя из распределения молекул по скоростям
(рис. 65). Исходя из распределения молекул по скоростям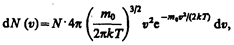 (44.4)
(44.4)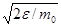 и d v=
и d v= 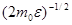 d e, получим
d e, получим