Лабораторная работа №6
Тема: Разработка программ с использованием процедур и функций.
Цель работы: изучить работу процедуры и функции и обрести навык написания программ с применением процедур и функций. 1. Основные понятия. Широко распространена в программах форма повторяемости, когда одна и та же последовательность действий должна выполняться на различных этапах информации. В программах такого рода в различных местах встречаются фрагменты, одинаковые по выполняемым действиям и различающиеся только в значениях исходных данных. При составлении программы приходиться задавать одну и ту же группу операторов, соответствующую каждому из повторяющихся фрагментов. Для более эффективного программирования подобных повторений в языке введено понятие подпрограммы. Повторяющаяся группа операторов оформляется в виде самостоятельной единицы – подпрограммы, записывается однократно, а в соответствующих местах программы обеспечивает лишь обращение к ней. Использование аппарата подпрограммы позволяет сократить объем и улучшить структуру программы с точки зрения наглядности и читаемости. Подпрограмма может быть рассмотрена как самостоятельная программа (со своими входными и выходными данными). В языке Паскаль подпрограммы реализуются в виде процедур и функций, которые вводятся в программу с помощью своего описания. 1.1. Описание процедуры. Процедуры описываются в специальном разделе описательной части программы вслед за разделом переменных. Любая процедура состоит, аналогично программе, из заголовка процедуры и блока. Заголовок процедуры представляет собой: PROCEDURE <ИМЯ> (<СПИСОК ПАРАМЕТРОВ>), где PROCEDURE – служебное слово, ИМЯ – имя процедуры, СПИСОК ПАРАМЕТРОВ - перечень имен для обозначения исходных данных и результатов работы процедуры с указанием их типов. Параметры, перечисленные в списке, называются формальными. Допускается описание процедуры, несодержащей формальных параметров: PROCEDURE <ИМЯ>; Содержательная часть процедуры представляет собой блок и состоит, следовательно, из раздела описаний (меток, констант, типов, переменных, процедур, и функций) и раздела операторов, представляющего собой составной Если в заголовке процедуры параметры указаны без слова VAR, то это параметры-значения. Параметры-значения могут изменяться внутри процедуры, но для внешней программы это изменение окажется незамеченным. Для получения результатов в основной программе используются параметры-переменные. Эти параметры перечисляются после служебного слова VAR с обязательным указанием типа. Тело процедуры состоит: 1) из описательной части, где определена переменная I, необходимая и имеющая смысл только внутри данной процедуры и называемая локальной переменной (значение локальной переменной недоступно в основной программе); 2) из составного оператора BEGIN-END, реализующего алгоритм вычисления степени действительного числа с натуральным показателем. 1.2. Функция. Функция – это подпрограмма, результат выполнения которой есть единственное скалярное значение, присваиваемое имени этой функции. Следовательно, функции являются частным случаем процедур и принципиально отличаются от них тем, что, во-первых, результат выполнения функции – одно значение, а процедуры – одно или несколько; во-вторых, результат выполнения функции передается в основную программу, как значение имени этой функции, а результаты выполнения процедуры – как значения ее параметров. Описание функции аналогично описанию процедуры и состоит из заголовка и блока. Заголовок функции имеет вид: FUNCTION <ИМЯ> (<СПИСОК ПАРАМЕТРОВ>):<ТИП> где FUNCTION – служебное слово, ИМЯ – имя функции, СПИСОК ПАРАМЕТРОВ – перечень формальных параметров (исходных данных) с указанием их типов, ТИП – тип результата: значение, которое должно приобретать имя функции. Допускается описание функции без параметров: FUNCTION <ИМЯ>: <ТИП>; В содержательной части программы-функции имени должно быть присвоено некоторое значение (значение ответа), т.е. имя хотя бы один раз должно присутствовать в левой части некоторого оператора присваивания. 1.3. Обращение к подпрограммам. Описание процедуры (или функции), расположенное в разделе описаний, само по себе никакого действия не вызывает. Чтобы исполнить процедуру (или функцию), необходимо в нужном месте программы поместить обращение к ней. Обращение к процедуре производится с помощью оператора процедуры, имеющего вид: <ИМЯ> (<СПИСОК АРГУМЕНТОВ>); где ИМЯ – имя процедуры, к которой происходит обращение, СПИСОК АРГУМЕНТОВ – перечень конкретных значений (выражений) и имен, подставляемых на место формальных параметров процедуры при ее выполнении. При вызове процедуры формальные параметры, указанные в заголовке, заменяются аргументами в порядке их следования: первому слева параметру в списке ставится в соответствие первый аргумент, второму – второй и т.д. Аргументы, перечисленные в операторе процедуры, называются также фактическими параметрами. Число, тип и порядок следования формальных и фактических параметров должно совпадать. Структура программы, содержащей процедуру, имеет вид: Program <имя>;
Формальные параметры – это переменные, фиктивно (формально) присутствующие в процедуре и определяющие тип и место подстановки фактических параметров. Фактические параметры – это реальные объекты (программы, заменяющие в теле процедуры при ее вызове формальные параметры). Над этими объектами и производятся действия, предусмотренные операторами тела процедуры. Имена формальных и фактических параметров целесообразно выбирать различными, что сделает программу более наглядной. Обращение к функции осуществляется аналогично обращению к стандартным функциям (sin, cos, tan и т.д.) и является разновидностью операнда в выражениях в отличие от вызова процедуры, являющегося разновидностью оператора. В этом месте выражения, где это необходимо, записывается имя функции, вслед за которым в скобках перечисляются фактические параметры. Если вызывается функция без параметров, то указывается только ее имя.
2. Задание 2.1 Из таблицы 1. По номеру варианта взять задание и составить программу, используя подпрограмму- процедуру. 2.2 Из таблицы 2 по номеру варианта взять задание и составить программу, используя подпрограмму FUNCTION.
Контрольные вопросы: 1. Заголовок процедуры и функции. 2. Что входит в тело процедуры? 3. Отличия процедуры и функции. 4. Понятия локальной и глобальной переменной. 5. Обращение к подпрограммам. 6. Какие параметры являются фактическими, какие формальными? 7. Параметры процедур и функций. 8. Соответствие между формальными и фактическими параметрами. Литература 1. Новичков В.С. ПАСКАЛЬ – В.С. Новичков, Н.И. Парфилов, А.Н. Пылькин - М.: Высш. школа, 1990г. 223 стр. 2. Савельев А.Я. ЯЗЫКИ ПРОГРАММИРОВАНИЯ (Паскаль, ПЛ/М). – М.:Высш. школа. 1987г. –143 стр. 3. Боон К. ПАСКАЛЬ ДЛЯ ВСЕХ. – М.- Энергоатомиздат, 1988г.- 190 стр. Таблица 1
Таблица 2
|



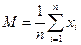

 , где
, где 

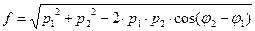 , где
, где  и
и 
 , где
, где  корни уравнения
корни уравнения  ;
;  - корни уравнения
- корни уравнения  . Корни уравнения находятся в подпрограмме- процедуре. Если корни мнимые, то считать их равными нулю. Исходные данные: A=0,5; B=3; C=1;
. Корни уравнения находятся в подпрограмме- процедуре. Если корни мнимые, то считать их равными нулю. Исходные данные: A=0,5; B=3; C=1;
 r - полупериметр треугольника NKM. Исходные данные: а=3; b=2,5; c=1,7; d=2; e=7,8; f=7
r - полупериметр треугольника NKM. Исходные данные: а=3; b=2,5; c=1,7; d=2; e=7,8; f=7
 вычисляются по формулам:
вычисляются по формулам:  ,
,  и
и  . Исходные данные: n=6; r=3; i=1,2….n
. Исходные данные: n=6; r=3; i=1,2….n
 где
где  заданы массивом;
заданы массивом;
 =(0,2; 0,46; 0,33; 0,97; 0,15; 0,61; 0,54; 0,77)
=(0,2; 0,46; 0,33; 0,97; 0,15; 0,61; 0,54; 0,77)
 где X=
где X=  S=
S=  элементы массива.
Исходные данные:n=3; m=8; i=1,.2..m;
=(5,6; 0,3; -0,9; 3; 2,8; 1,45; -4,6; 1)
элементы массива.
Исходные данные:n=3; m=8; i=1,.2..m;
=(5,6; 0,3; -0,9; 3; 2,8; 1,45; -4,6; 1)

 где r-полупериметр треугольника MNK.
Исходные данные j=1; c=2,5; i=2,7; a=1; b=2,7; d=3,2.
где r-полупериметр треугольника MNK.
Исходные данные j=1; c=2,5; i=2,7; a=1; b=2,7; d=3,2.

 при а=4,5; b=0,7; c=6,2; А x принимает значения 0,2; 0,56; 0,83
при а=4,5; b=0,7; c=6,2; А x принимает значения 0,2; 0,56; 0,83
 , при a=0,8; b=0,16; c=0,4;
a=0,6; b=0,4; c=1,2;
a=0,47; b=0,1; c=0,5.
, при a=0,8; b=0,16; c=0,4;
a=0,6; b=0,4; c=1,2;
a=0,47; b=0,1; c=0,5.
 , при a=0,15; b=1,5;
a=1,7; b=0,1.
, при a=0,15; b=1,5;
a=1,7; b=0,1.
 , при x=1,4; y=0,8;
x=0,9; y=0,6;
x=2,9; y=0,4; a d=5,3, при всех значениях x,y.
, при x=1,4; y=0,8;
x=0,9; y=0,6;
x=2,9; y=0,4; a d=5,3, при всех значениях x,y.
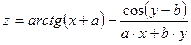 , при x=0,4; y=1,2;
x=0,25; y=1,3;
a=0,54; b=1 при всех значениях x, y
, при x=0,4; y=1,2;
x=0,25; y=1,3;
a=0,54; b=1 при всех значениях x, y
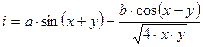 , при a=10,7; b=6,3; y=0,35; a x принимает значения 0,6; 0,51; 0,42.
, при a=10,7; b=6,3; y=0,35; a x принимает значения 0,6; 0,51; 0,42.
 , при x=3; y=4;
x=1,6; y=5,8;
x=4,5; y=2,7; a=7,1; b=2,4 при всех значениях x, y
, при x=3; y=4;
x=1,6; y=5,8;
x=4,5; y=2,7; a=7,1; b=2,4 при всех значениях x, y
 , при x=0,1; y=0,7;
x=0,4; y=0,6
x=0,5; y=0,2; a=2; b=0,1 при всех значениях x, y
, при x=0,1; y=0,7;
x=0,4; y=0,6
x=0,5; y=0,2; a=2; b=0,1 при всех значениях x, y
 , при a=9,7; b=2,7, a x принимает значения 4,8; 9,6; 0,44.
, при a=9,7; b=2,7, a x принимает значения 4,8; 9,6; 0,44.
 , при x=0,35; y=0,1;
x=0,82; y=0,12;
x=0,67; y=0,3, a=0,24;
b=4,9 при всех значениях x, y.
, при x=0,35; y=0,1;
x=0,82; y=0,12;
x=0,67; y=0,3, a=0,24;
b=4,9 при всех значениях x, y.
 , при a=4; b=2,7, a x принимает значения 0,1; 0,25; 0,14; 0,21.
, при a=4; b=2,7, a x принимает значения 0,1; 0,25; 0,14; 0,21.







