Лабораторная работа №3. Тема: Программирование циклических структур алгоритма.

 

Тема: Программирование циклических структур алгоритма.

Цель работы: Познакомиться с операторами цикла, научиться применять их при составлении программ.

1. Теоретические сведения.

1.1. Понятие циклического процесса.

Если вычислительный процесс содержит многократные вычисления по одним и тем же математическим зависимостям, но для различных значений, входящих в них величин (переменных), то его называют циклическим. Многократно повторяемые участки вычислений называют циклами, а переменные, изменяющиеся в цикле, - переменными цикла. Алгоритм циклической структуры в общем виде должен содержать:

1) подготовку цикла: задание начальных значений переменным цикла перед первым его выполнением;

2) тело цикла: действия, повторяемые в цикле для различных значений переменных цикла;

3) модификацию (изменение) значений переменных цикла перед каждым новым его повторением;

4) управление циклом: проверку условия продолжения (или окончания) цикла и переход на начало тела цикла, если выполняется условие продолжения цикла (или выход из цикла по его окончании).

Программно цикл может быть реализован с помощью операторов присваивания, if, goto. Однако в языке Паскаль для этой цели существуют специальные операторы цикла, которые обеспечивают более компактную, наглядную запись алгоритма, позволяют создавать более эффективные программы.

1.2 Операторы цикла с присваиванием.

Различают циклы с заданным и заранее неизвестным числом повторений. Циклы первого типа называют также циклами со счетчиком. Число повторений тела цикла в этом случае подсчитывается с помощью специальной переменной (счетчика), для которой известны начальное и конечное значения, шаг её изменения. Управление циклом осуществляется на основании сравнения текущего значения счетчика с конечным. Переменную – счетчик именуют параметром цикла, а сам цикл – циклом с параметром.

Оператор цикла с параметром имеет следующий вид:

For i:=m1 to m2 do s или

For i:=m1 down to m2 do s

Где for (для), To (до), Downto (вниз до), Do(выполнить) – служебные слова;

I – параметр цикла (переменная любого скалярного типа, кроме вещественного);

M1, m2 – начальное и конечное значения параметра цикла (тип, который должен совпадать с типом параметра цикла);

S – тело цикла, которое может содержать один или несколько операторов.

Работа оператора цикла при использовании служебного слова To заключается в следующем. Параметр цикла принимает начальное значение (m1) и сравнивается с конечным значением (m2).Если параметр цикла не превышает значения m2, то управление передаётся в тело цикла и операторы выполняются. Затем значение параметра цикла увеличивается на единицу, и работа повторяется. Выход из цикла выполнится после того, как значение параметра цикла превысит конечное значение m2.

При использовании в операторе цикла служебного слова Downto параметр цикла будет изменяться в обратном порядке: с шагом – 1.

Оператор цикла for следует использовать во всех случаях, когда заранее известно число повторений или его можно подсчитать.

При программировании циклов с параметрами необходимо помнить следующие правила организации цикла:

1) параметры цикла, начальное и конечное значения, должны быть одинакового типа, их тип может быть любым скалярным типом (стандартным, перечисляемым, ограниченным), кроме вещественного;

2) очередное значение параметра цикла вычисляется автоматически с помощью функции SUCC в сочетании с TO или PRED в сочетании с DOWNTO; в частности для целого типа шаг изменения значения параметра цикла равен 1 при TO и -1 при DOWNTO;

3) запрещено изменять внутри (в теле) цикла значение параметра цикла, начальное и конечное значение;

4) запрещено входить в цикл с помощью оператора GOTO, минуя оператор FOR, так как значение переменной параметра цикла, начальное и конечное значения будут не определены;

5) цикл не выполняется вообще, если начальное значение больше (при DOWNTO - меньше), чем конечное;

6) по окончанию выполнения цикла значение переменной параметра неопределенно и не может быть использовано в дальнейших вычислениях;

7) после служебного слова DO может стоять только один оператор; если в цикле нужно выполнить группу операторов, то их заключают в операторные скобки BEGIN-END;

8) из составного оператора, входящего в оператор цикла, можно выйти до окончания этого цикла с помощью GOTO, тогда последнее значение параметра цикла сохраняется.

1.3. Оператор цикла с предусловием.

Оператор цикла с предусловием имеет следующий вид:

WHILE В DO S

где WHILE (пока), DO (выполнить) - служебные слова;

В - условие (логическое выражение)

S - тело цикла, содержащие один или несколько операторов.

Работа оператора цикла WHILE заключается в следующем.

Если условие истинно, то выполняются операторы, входящие в тело цикла. Как только условие станет ложным, выполнение операторов цикла прекращается. Если условие ложно с самого начала, то оператор цикла не выполняются ни разу. Условие вычисляется и анализируется перед каждым выполнением цикла, отсюда и термин “предусловие”. Значения переменных, входящих в условие, должны изменяться в теле цикла, иначе, цикл никогда не завершится.

Оператор цикла WHILE позволяет организовать цикл с неизвестным числом повторений, т.к. оно зависит от вычислений в операторе.

1.4. Оператор цикла с постусловием.

Оператор цикла с постусловием имеет следующий вид:

REPEAT

S1;

S2;

...

UNTIL B

Где REPEAT (повторять), UNTIL (до тех пор, пока) – служебные слова;

S1, S2... любые операторы языка, входящие в тело цикла;

B – условие (логическое выражение).

Действие оператора REPEAT подобно действию оператора WHILE, но проверка условия производится после очередного цикла, что обеспечивает его выполнение хотя бы один раз. Служебные слова REPEAT, UNTIL по действию похожи на операторные скобки BEGIN – END. Между ними можно поместить группу операторов, отделяя их друг от друга точкой с запятой. Операторы, входящие в тело цикла выполняются до тех пор, пока условие ложно.

При составлении циклов с предусловием или постусловием необходимо принимать во внимание следующие моменты:

1) перед каждым выполнением цикла условие его окончания (или продолжения) должно быть определено (иметь конкретное значение);

2) тело цикла должно содержать хотя бы один оператор, влияющий на условие окончания (продолжения), иначе цикл будет продолжаться бесконечно;

3) условие окончания цикла должно быть в конце концов удовлетворено;

4) условие вычисляется при каждом выполнении цикла и поэтому должно быть насколько можно простым.

1.5. Вложенные циклы.

Если телом цикла является циклическая структура, то такие циклы называют вложенными или сложными. Цикл, содержащий в себе другой цикл, называют внешним. Цикл, содержащийся в теле другого цикла, называют внутренним. Внутренний и внешний цикл могут быть любыми из трёх рассмотренных видов: цикл с параметром, цикл с предусловием, цикл с постусловием. Правила организации, как внешнего, так и внутреннего циклов такие же, как и для простого цикла каждого из этих видов. Однако при построении вложенных циклов необходимо соблюдать следующее условие: все операторы внутреннего цикла должны полностью лежать в теле внешнего цикла. Сложные циклы условно разбивают на уровни вложенности.

Параметры циклов разных уровней изменяются не одновременно. Вначале все свои значения изменит параметр цикла наивысшего уровня вложенности при фиксированных (начальных) значениях параметров циклов с меньшим уровнем. Затем изменяется на один шаг значение параметра цикла следующего уровня и снова полностью выполняется самый внутренний цикл и т. д. до тех пор, пока параметры циклов всех уровней не примут все требуемые значения.

2. Задание

Взять задание из таблицы 1 согласно варианта. Составить блок-схему алгоритма и программу для вычисления суммы членов бесконечного ряда с точностью до члена ряда, меньшего ε=0,001 при заданных значениях Х.

 

Контрольные вопросы.

1. Что представляет собой циклический вычислительный процесс?

2. Общий вид операторов цикла с параметром?

3. Правила организации цикла с параметром?

4. Общий вид оператора цикла с постусловием. В чем отличие данного оператора от оператора цикла с предусловием?

5. Общий вид оператора цикла с предусловием. Когда применяется данный оператор?

6. Какие циклы называются вложенными?

7. Понятие уровня вложенности в сложных цикла.

8. Как изменяются параметры циклов разных уровней вложенности?

 

Литература.

1. Новичков В.С. Алгоритмические языки в техникуме. - М.: Высшая школа, 1990-222с.

2. Боон К. Паскаль для всех. – М.: Энергоатомиздат, 1988.-188с.

3. Савельев А.Я. Языки программирования (Паскаль. ПЛ/М). – М.: Высшая школа, 1987.-142с.

Таблица 1.

Номер Варианта	Содержание задания
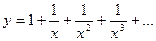1.	При Х изменяющемся от –2 до 4 с шагом 0,2
2.	При Х изменяющемся от –0,1 до –2 с шагом –0,3
3.	При Х изменяющемся от –1 до 1 с шагом 1
4.	При Х изменяющемся от 0,1 до 1 с шагом 0,1
5.	При Х изменяющемся от 0,2 до 1 с шагом 0,1
6.	При Х изменяющемся от –0,5 до 1 с шагом 0,5
7.	При Х изменяющемся от –π до π с шагом π /6
8.	При Х изменяющемся от – π /2 до π /2 с шагом π /8
9.	При Х изменяющемся от –2 до 1 с шагом 0,5
10.	При Х изменяющемся от –1 до 1 с шагом π /10
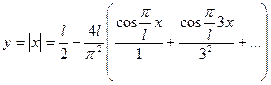11.	При Х изменяющемся от –L до L с шагом 2
12.	При Х изменяющемся от – π /2 до π /2 с шагом π /10
13.	При Х изменяющемся от –1 до –2 с шагом –0,2
	При Х изменяющемся от –1 до -2 с шагом -0,2
15.	При Х изменяющемся от –1 до –1,5 с шагом –0,1
16.	При Х изменяющемся от 0,8 до 1,6 с шагом 0,2
17.	При Х изменяющемся от 0,5 до 2,5 с шагом 0,5
18.	При Х изменяющемся от – π /2 до π /2 с шагом π /10
19.	При Х изменяющемся от 0 до π с шагом π /8
20.	При Х изменяющемся от – π /2 до π /2 с шагом π /10
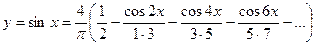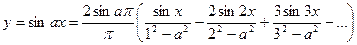21.	При Х изменяющемся от – π до π с шагом π /10
22.	При Х изменяющемся от – π /2 до π /2 с шагом π /8
23.	При Х изменяющемся от 1,2 до 2,2 с шагом 0,2
24.	При Х изменяющемся от – π /2 до π /2 с шагом π /10
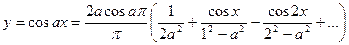25.	При Х изменяющемся от 0 до –0,5 с шагом –0,1