Определение зависимости прогиба прямоугольных конструкций от геометрических размеров образца
Лабораторная работа ИЗУЧЕНИЕ УПРУГИХ СВОЙСТВ ТВЕРДЫХ ТЕЛ Цель работы: определение характеристик упругости стали и дерева по их деформации на растяжение и изгиб; определение зависимости прогиба прямоугольных конструкций от геометрических размеров образца ЭЛЕМЕНТЫ ТЕОРИИ
Все реальные тела под действием внешних сил деформируются, т.е. изменяют свою форму и размеры. Различаются деформации растяжения (сжатия), сдвига, изгиба, кручения и более сложные виды деформации, которые всегда можно свести к двум: растяжение (сжатие) и сдвиг. Если деформации исчезают после прекращения действия приложенных сил, то они называются упругими. Деформации, частично сохраняющиеся после снятия нагрузки, называются неупругими или пластическими. В настоящей работе рассматриваются только процессы, протекающие в материале при упругих деформациях.
Рассмотрим деформацию растяжения однородного круглого стержня AB длиной l0, один конец которого жестко закреплен. Если к другому концу стержня приложить силу x = Dl = l – l0 (1) и относительное удлинение
Опыт показывает, что при деформации растяжения или сжатия изменяются также и поперечные размеры стержня. Пусть d0 и d – диаметры стержня до и после деформации растяжения. При деформации растяжения диаметр стержня уменьшается, т.е. d < d0. Величина
называется относительным поперечным сжатием стержня. Относительное изменение объема стержня
так как e и d много меньше единицы, и их произведениями можно пренебречь. Величина, равная отношению относительного поперечного сжатия к соответствующему относительному продольному удлинению называется коэффициентом Пуассона:
Коэффициент Пуассона m зависит только от материала тела и является одной из важных характеристик его упругих свойств. Выделим мысленно в стержне некоторое поперечное сечение C площадью S. Часть BC стержня находится в равновесии. Следовательно, в выделенном сечении со стороны другой части стержня AC действует упругая сила Для характеристики деформированного состояния стержня вводят понятие нормального напряжения, которое численно равно упругой силе, действующей на единицу площади сечения, перпендикулярного силе.
где dFу – упругая сила, перпендикулярная элементарной площадке dS, в пределах которой деформацию можно считать однородной. Отметим, что сила упругости направлена противоположно направлению абсолютного удлинения. При однородной деформации нормальное напряжение одинаково в любой точке поперечного сечения стержня. Как показывает опыт, при малых деформациях между нормальным напряжением и относительным удлинением существует прямая пропорциональная зависимость s = Ee. (7) Коэффициент пропорциональности E характеризует упругие свойства вещества и называется модулем продольной упругости или модулем Юнга. Модуль продольной упругости численно равен нормальному напряжению, которое возникает в теле при его относительном удлинении, равном единице, т.е. при увеличении длины стержня в два раза. Формула (7) выражает закон Гука, который формулируется следующим образом: в пределах упругости напряжение, возникающее в теле, прямо пропорционально относительной деформации. Модуль Юнга Е и коэффициент Пуассона m полностью характеризуют упругие свойства изотропного вещества. Все остальные упругие постоянные могут быть выражены через Е и m. Из (2), (6) и (7) следует, что при однородной деформации растяжения модуль силы упругости
или
где k– коэффициент упругости стержня, определяемый как
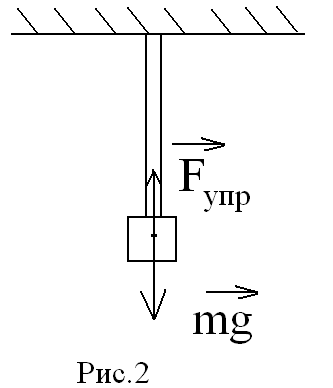
Следует отметить, что закон Гука выполняется только на начальных стадиях деформации. Для каждого материала существует критическое нормальное напряжение, называемое пределом пропорциональности [ ], превышение которого приводит к тому, что деформация еще может считаться упругой (остаточная деформация образцов не превышает 5%), но закон Гука уже не выполняется. Рассмотрим возможности расчетов характеристик упругих свойств материалов на примере двух наиболее часто встречающихся на практике типов деформации: деформации растяжения и деформации изгиба. Деформация растяжения. Пусть проволока диаметром поперечного сечения d, начальной длины l0 , изготовленная из исследуемого материала, растягивается под действием груза массой m. При этом в материале возникают силы упругости, определяемые по закону Гука (рис.2).
Согласно условию статического равновесия
Учитывая (9), получим
Поперечное сечение стержня на практике удобно рассчитывать по измеренному микрометром диаметру проволоки d
Равенство (10)в этом случае можно представить в виде
откуда
где коэффициент пропорциональности a – практически постоянная для данного образца величина. Если, изменяя массу груза m, каждый раз измерять абсолютное удлинение проволоки Dl и построить график Dl = f(m), то можно убедиться в справедливости закона Гука. По наклону графика D(Dl)/Dm легко определить коэффициент пропорциональности a в (11) и рассчитать модуль продольной упругости (модуль Юнга) проволоки:
Для уменьшения погрешности интервал нагрузок Dm и соответствующий ему интервал абсолютных удлинений D(Dl) на графике следует выбирать по возможности большими (но в пределах пропорциональности).
|


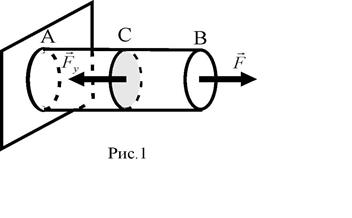
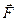 (рис. 1), его длина станет l. В качестве меры деформации растяжения служит абсолютное удлинение
(рис. 1), его длина станет l. В качестве меры деформации растяжения служит абсолютное удлинение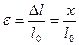 . (2)
. (2) (3)
(3) , (4)
, (4) . (5)
. (5) , равная по модулю внешней силе. Поскольку положение сечения С выбрано произвольно, то это значит, что упругая сила, действующая в любом поперечном сечении стержня равна по модулю внешней силе.
, равная по модулю внешней силе. Поскольку положение сечения С выбрано произвольно, то это значит, что упругая сила, действующая в любом поперечном сечении стержня равна по модулю внешней силе. , (6)
, (6)
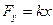 , (8)
, (8) (9)
(9)

 (10)
(10)
 ,
, (11)
(11) (12)
(12)


