Сведение исходной задачи к краевой
Принцип максимума является необходимым, условием оптимальности. Если исключить управление
Таким образом, если задача (1), (2) имеет решение, то оптимальная траектория находится среди решений краевой задачи (5). В сведении вариационной задачи (задача минимизации функционала) к краевой задаче для обыкновенных дифференциальных уравнений и состоит конечный результат применения принципа максимума к задаче оптимального управления. В общем случае принцип максимума не является достаточным условием оптимальности: ему могут удовлетворить и не оптимальные управления.
3. Простейшая задача с нефиксированной продолжительностью процесса Пусть момент
которые непрерывны всюду при
Задача оптимальности состоит в поиске среди
Теорема 2. Для того, чтобы число
Здесь
|
из условия максимума, то есть найти такую функцию 
, что 
и подставить результат в уравнение (I), (3), то получим следующую краевую задачу для системы из 
уравнений (краевая задача):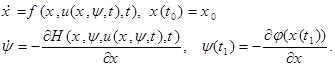
(5)
окончания процесса в системе 
нефиксирован. Тогда простейшая задача несколько изменится. Допустимыми управлениям называются 
-мерные функции
, (6)
за исключением, возможно, конечного числа точек на каждом ограниченном отрезке, где они имеют разрывы первого рода. Критерий качества теперь может явно зависеть от длительности процесса.
. (7)
и доступных управлений оптимального момента 
и оптимального управления 
, на которой критерий качества (7) достигает минимального значения
и управление 
, 
доставляли решение задаче (1), (6), (7) необходимо, чтобы выполнялись условия:
.
-оптимальная траектория (решение уравнения (1) при 
) 
-решение уравнения
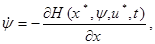при 
.
