Усложним простейшую задачу добавлением ограничений на правый конец допустимой траектории. Рассмотрим процесс, описываемый уравнением (1).
Как в основной задаче оптимального управления будем рассматривать в качестве допустимого управления 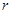 -мерно-кусочно-непрерывную функцию
-мерно-кусочно-непрерывную функцию  удовлетворяющую ограничению
удовлетворяющую ограничению  .
.
Пусть  - вещественные функции, определённые на
- вещественные функции, определённые на  и
и  функции класса
функции класса  . Зададим область
. Зададим область
 .
.
Будем искать допустимое управление  ,
,  со значениями из заданного множества
со значениями из заданного множества 
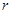 - мерного пространства, для которых траектория
- мерного пространства, для которых траектория 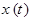 ,
,  системы (1) в момент
системы (1) в момент  попадают в множество
попадают в множество  (задача с ограничениями на правый конец траектории).
(задача с ограничениями на правый конец траектории).
Теорема 3. Пусть 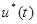 и
и  соответствующие оптимальные управление и траектория в задаче терминального управления с ограничениями на правый конец траектории. Тогда найдутся такие числа
соответствующие оптимальные управление и траектория в задаче терминального управления с ограничениями на правый конец траектории. Тогда найдутся такие числа  и не все равные нулю одновременно, такие, что вдоль оптимальной траектории
и не все равные нулю одновременно, такие, что вдоль оптимальной траектории  и решения
и решения  сопряженной системы уравнений
сопряженной системы уравнений  , выполняются условия:
, выполняются условия:
1) условия максимума 
2) условия трансверсальности 
Если имеются ограничения на левый конец траектории, тогда найдутся  - вещественные функции, определённые на
- вещественные функции, определённые на  и
и  функции класса
функции класса  . Зададим область
. Зададим область 
Будем искать допустимое управление  ,
,  со значениями из заданного множества
со значениями из заданного множества 
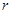 - мерного пространства, для которых траектория
- мерного пространства, для которых траектория 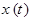 ,
,  системы (1) в момент
системы (1) в момент  попадают в множество
попадают в множество  (задача с ограничениями на левый конец траектории).
(задача с ограничениями на левый конец траектории).
Теорема 4. Пусть 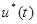 и
и  соответствующие оптимальные управление и траектория в задаче терминального управления с ограничениями на левый конец траектории. Тогда найдутся такие числа
соответствующие оптимальные управление и траектория в задаче терминального управления с ограничениями на левый конец траектории. Тогда найдутся такие числа  и не все равные нулю одновременно, такие, что вдоль оптимальной траектории
и не все равные нулю одновременно, такие, что вдоль оптимальной траектории  и решения
и решения  сопряженной системы уравнений
сопряженной системы уравнений  , выполняются условия:
, выполняются условия:
1) условия максимума 
2) условия трансверсальности  .
.

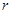 -мерно-кусочно-непрерывную функцию
-мерно-кусочно-непрерывную функцию  удовлетворяющую ограничению
удовлетворяющую ограничению  .
. - вещественные функции, определённые на
- вещественные функции, определённые на  и
и  функции класса
функции класса  . Зададим область
. Зададим область .
. ,
,  со значениями из заданного множества
со значениями из заданного множества 
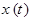 ,
,  попадают в множество
попадают в множество  (задача с ограничениями на правый конец траектории).
(задача с ограничениями на правый конец траектории).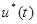 и
и  соответствующие оптимальные управление и траектория в задаче терминального управления с ограничениями на правый конец траектории. Тогда найдутся такие числа
соответствующие оптимальные управление и траектория в задаче терминального управления с ограничениями на правый конец траектории. Тогда найдутся такие числа  и не все равные нулю одновременно, такие, что вдоль оптимальной траектории
и не все равные нулю одновременно, такие, что вдоль оптимальной траектории  сопряженной системы уравнений
сопряженной системы уравнений  , выполняются условия:
, выполняются условия:

 - вещественные функции, определённые на
- вещественные функции, определённые на  функции класса
функции класса 
 системы (1) в момент
системы (1) в момент  попадают в множество
попадают в множество  (задача с ограничениями на левый конец траектории).
(задача с ограничениями на левый конец траектории). и не все равные нулю одновременно, такие, что вдоль оптимальной траектории
и не все равные нулю одновременно, такие, что вдоль оптимальной траектории 
 .
.


