Задача оптимального быстродействия с закрепленными концамиВ силу особой распространенности задачи быстродействия сформулируем для нее отдельно необходимые условия оптимального управления. Теорема 9. Для того, чтобы допустимое управление
необходимо, чтобы выполнялись: 1) условие максимума для некоторого нетривиального решения 2) условие для оптимального момента Пример 1. Перевести точку Решение. Используем теорему 4. В нашем случае граничными условиями трансверсальности
Условие максимума Условие для оптимального момента Пример 2. Пусть требуется минимизировать функционал
при условиях:
Решение. Строим функцию Гамильтона:
Условие максимума:
Следовательно: Решим это дифференциальное уравнение:
Воспользуемся граничными условиями для нахождения
Тогда траектория соответствующая оптимальному управлению примет вид:
Оптимальное управление:
Задание к лабораторной работе №13.
Минимизировать функционалы 1.
2. 3. 4.
5. 6. 7. 8.
9. 10. 11.
12. 13. 14. 15.
16. 17. 18.
19. 20. 21.
22.
23. 24. 25.
|
, 
, было решением задачи быстродействия
,
,
системы 
из состояния 
на множество 
быстрейшим образом, предполагая, что движение точки подчиняется уравнениям 
причем 
. Начальный момент времени 
с
.
для некоторого нетривиального решения 
со знаком “+”, 
.
.
.
,
.
.
,
, 
,
.
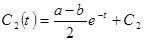
и 
: 
,
.
.
, 
.
,
, 
.
, 
.
, 
,
, 
.
, 
, 
.
, 
, 
, 
,
,
, 
, 
, 
, 
.
, 
.
, 
, 
.
,
, 
.
, 
.
, 
.
, 
, 
, 
, 
.
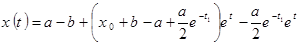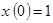